Александр Петров - Гравитация. От хрустальных сфер до кротовых нор

Часто считают, что этот принцип тоже лежит в основе общей теории относительности. Однако это не так однозначно. Даже сейчас, почти через 100 лет после создания ОТО, в профессиональной литературе время от времени выходят статьи с обсуждением роли этого принципа. Даже его название является предметом дискуссии.

Приведем один из аргументов, который вносит некое сомнение в само представление об эквивалентности в этом случае. Основным отличием пространства-времени ОТО от пространства-времени СТО является его кривизна, которая (как было сказано) определяется тензором кривизны. В пространстве-времени СТО этот тензор тождественно равен нулю, поэтому пространство Минковского называют плоским. Если применить сильный принцип эквивалентности (а понятию «эквивалентность» придать абсолютный смысл) для описания движения в ускоренной системе в пространстве Минковского, то нужно будет сказать, что от плоского пространства-времени мы перешли к искривленному пространству-времени ОТО. Но это невозможно, поскольку невозможно воссоздать из нулевой кривизны ненулевую лишь переходом между системами отсчета. «Малые размеры системы отсчета» в определении принципа не могут быть оправданием, поскольку кривизна – понятие локальное, она определяется в каждой точке.

Хотя в окончательную форму теории Эйнштейна сильный принцип эквивалентности не вошел, исторически он сыграл большую роль в становлении ОТО. Эйнштейн при разработке теории активно его использовал. Также, если в принципиальном плане нельзя из плоского мира сделать искривленный просто переходом в другую систему отсчета, то многие эффекты теории Эйнштейна действительно имеют место в ускоренных системах отсчета.

В качестве принципов построения теории, конечно, необходимы принципы соответствия . В чем они должны состоять? В случае слабых гравитационных полей (малой кривизны пространства-времени) и малых (по сравнению со световой) скоростей уравнения релятивистской теории гравитации должны перейти в уравнения гравитации Ньютона (их полевую форму мы обсудим несколько ниже). То есть предсказания общей теории относительности должны совпасть с результатами применения закона всемирного тяготения Ньютона с небольшими поправками, которые становятся значительными по мере увеличения напряженности поля и увеличения скоростей. В случае отсутствия гравитации (нулевая кривизна) уравнения новой теории тяготения должны перейти в уравнения СТО.

Наконец, иногда в качестве принципов, на основе которых была построена ОТО, упоминают ковариантность – требование, чтобы уравнения теории имели один и тот же вид во всех координатных системах. Это требование в определенном смысле является обобщением лоренц-инвариантности в СТО.

Фактически все принципиальные предпосылки и необходимые требования для формулировки уравнений гравитационного поля в ОТО мы обсудили. Было осознано, что гравитационное взаимодействие выражается в искривлении пространства-времени, а искривляется пространство-время под воздействием материи. Оказалось также, что и тела, и материя в целом, воздействуют на пространство-время не только своей массой (или, эквивалентно, энергией), но и состоянием движения, напряжениями внутри тел, взаимодействием между разными видами материи. Больше деталей о материальных источниках можно найти в Дополнении 2. С другой стороны, искривляя пространство-время, материя движется (взаимодействует) уже в пространстве-времени искривленном самой собой. То есть пространство-время в общем случае не является безучастной ареной, на которой кипят страсти физических взаимодействий, а само становится динамическим объектом и во всем участвует. Уравнения Эйнштейна как раз устанавливают правила воздействия материи на пространство-время и наоборот.

Эти уравнения были построены и представлены Эйнштейном в работах 1915 и 1916 годов на основании аргументов изложенных выше. Практически одновременно они были представлены немецким математиком Давидом Гильбертом (1862–1943). Научные интересы Гильберта во многом были связаны с математической физикой. С большим интересом он следил за попытками Эйнштейна создать общую теорию относительности, основанными на логике анализа физических явлений. Это вдохновило его на поиски строгого математического подхода к построению уравнений, которые и были выведены из, так называемого, принципа наименьшего действия. В общем, Гильберт имел планы «заковать физику» в рамки аксиоматического подхода. Но несмотря на впечатляющие результаты в построении уравнений гравитации, этот глобальный замысел Гильберта не удался. До сих пор ведутся споры о приоритете, однако мы считаем, что одни исследования дополняют другие. Если можно так сказать, то Эйнштейн проник в самую глубину физических явлений, а Гильберт дал аппарат, позволяющий исследовать их более эффективно.

Логика построения уравнений Эйнштейна и их конкретный формальный вид даны в Дополнении 3, а здесь мы разъясним основные понятия ОТО, к которым будем часто обращаться в основном тексте. Вернемся к понятию интервала, который был введен для пространства Минковского. В отличие от плоского пространства, в искривленном пространстве-времени расстояние между двумя мировыми точками в общем случае невозможно определить как конечную длину отрезка прямой. Необходимо перейти к измерениям в малой окрестности мировой точки (к бесконечно малым величинам). Тогда квадрат интервала пространства Минковского между двумя бесконечно близкими точками перепишется как квадрат элемента интервала (уже бесконечно малой величины) в виде:

ds 2= c 2 dt 2– dx 2– dy 2– dz 2.

Элемент пространства Минковского имеет такой простой вид еще и потому, что здесь используются координаты Лоренца, то есть декартовы координаты в совокупности с временной координатой. Этот же квадрат элемента интервала (часто его все равно называют «интервал») может быть записан в более формальном виде:

ds 2= η abdx adx b .

Здесь a, b = 0, 1, 2, 3; а нулевой координате обычно приписывают смысл временной, умноженной на скорость света: x 0= ct . Величина η ab является диагональной (отличны от нуля только элементы на диагонали) матрицей 4 × 4,

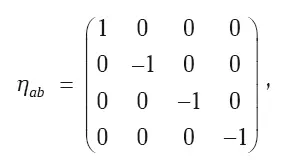
и называется метрикой Минковского. Формальная запись интервала перейдет в уже привычную, если использовать простое правило суммирования по повторяющимся индексам, например: m a n a = m 0 n 0+ m 1 n 1+ m 2 n 2+ m 3 n 3. Метрика η ab задает способ измерения расстояний в пространстве Минковского в лоренцевых координатах.