Александр Петров - Гравитация. От хрустальных сфер до кротовых нор

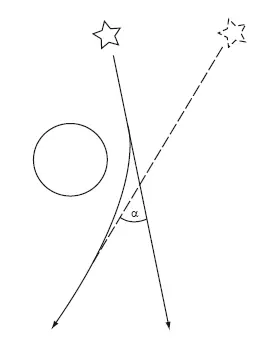
Рис. 7.1. Отклонение луча звезды в гравитационном поле Солнца

Хотя приведенная формула не была опубликована, она фигурировала в переписке нескольких ученых. Наконец, в 1801 году немецкий астроном Иоганн Георг фон Зольднер (1776–1833) представил в Берлинский астрономический ежегодник статью об отклонении луча света в гравитационном поле звезды, которая была опубликована в 1804 году и содержала эту замечательную формулу. Однако даже после публикации, она осталась на долгое время забытой.

О формуле Зольднера вспомнили в 1911 году, когда Эйнштейн в рамках специальной теории относительности получил точно такую же. К началу XX века телескопы уже давали возможность измерить угол отклонения луча света вблизи Солнца. Однако для такого измерения было необходимо затмение Солнца Луной, чтобы были видны звезды вблизи его края. Группа астрономов из Берлинской обсерватории заинтересовалась предсказаниями Эйнштейна и собралась провести измерения во время предстоящего полного солнечного затмения в Крыму в августе 1914 года, но началась Первая мировая война. А теория тем временем развивалась. В 1915 году на основе уже общей теории относительности, Эйнштейн получил новое значение для угла отклонения:

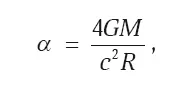
в два раза большее зольднеровского или своего 1911 года. Последовательный вывод этой формулы производится с помощью решения Шварцшильда. Уравнение траектории луча задается, как светоподобная геодезическая в пространстве-времени Шварцшильда, она имеет простой вид: ds 2= 0. Единственным исходным условием должно быть направление света далекой звезды на край Солнца, то есть при расчетах учитывается тот факт, что луч проходит от тяготеющего центра на расстоянии радиуса Солнца R .

Итак, после этого заявления Эйнштейна нужно было проверять обе формулы. Наконец, во время ближайшего полного солнечного затмения 29 мая 1919 года группой английских астрономов измерения отклонения луча света были произведены. Перед группой стояла задача после сделанных наблюдений выбрать один из трех следующих ответов:

1) гравитационное поле Солнца не оказывает влияния на траекторию луча света;

2) гравитационное поле Солнца действует на световой луч как на обычные частицы в силу закона тяготения Ньютона, что приводит к кажущемуся смещению изображения звезды у края солнечного диска, равному 0,87 ″ ;

3) отклонение изображения звезды согласуется с предсказаниями общей теории относительности и равно 1,75 ″ .

В пределах ошибок измерений был подтвержден третий ответ. И это было триумфом новой теории.

Смещение перигелиев планет. О смещении перигелия Меркурия мы уже говорили. В ОТО траектория планет также рассчитывается как движение массивной частицы по геодезическим в пространстве-времени Шварцшильда, окружающем Солнце. Расчет для массивных частиц немного сложнее, чем для световых. Необходимо знать массу планеты m , массу M центрального массивного тела (Солнца) и угловой момент планеты (последний определяется этими массами и эксцентриситетом e орбиты планеты). Расчет геодезической в пространстве-времени позволяет определить траекторию в пространстве. Эта траектория представляет собой вращающийся эллипс. Для орбиты с «неподвижным» эллипсом планета, начиная вращение от перигелия, за один оборот (2π) снова возвратится в перигелий. Для орбиты с «вращающимся» эллипсом это уже не так: за один оборот планета окажется в другой точке, при этом точка наименьшего удаления от Солнца («новый» перигелий) сместится. Угол между направлением из центрального тела на «старый» и «новый» перигелии равен

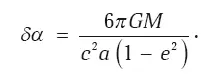
Получается, что кеплеровский эллипс сам начинает медленно вращаться, см. рис. 7.2. Формула определяет угловое перемещение за один период, то есть за один год этой планеты. За 100 земных лет у Меркурия накапливается величина 43,0 ″ , что находится в хорошем согласии с аномальным смещением, обнаруженным в середине XIX века, когда орбиты рассчитывались только с помощью закона Ньютона. У Земли за 100 земных лет смещение перигелия орбиты, вычисленное по этой формуле, равно 3,8 ″ . Оно также хорошо согласуется с наблюдениями.

Гравитационное красное смещение частоты сигнала. Чтобы перейти к третьему тесту необходимо определить, что такое истинное время, а что такое координатное время. Истинное время в данной точке – это время наблюдателя, его собственных часов. В какую точку наблюдателя не помещай, часы на его руке будут для него идти одинаково. Собственные биоритмы также не изменятся. У хорошо тренированных людей, например космонавтов, сердце одинаково стучит как на Земле, так и на орбите. Но на Земле мы ощущаем силу тяжести, в то время как космическая станция на орбите движется по геодезической (по инерции), является инерциальной системой отчета и там имеет место состояние невесомости. В отличие от истинного времени, координатное время не несет такой смысловой нагрузки. Оно вместе с пространственными координатами представляет как бы «сетку», накинутую на пространство-время, с помощью которой удобно производить измерения и не более.

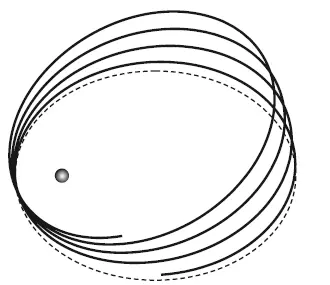
Рис. 7.2. Смещение перигелия Меркурия (пунктир – траектория по Ньютону)

Как связаны истинное время и координатное? Ограничимся рассмотрением статического пространства-времени, то есть такого, для которого все метрические коэффициенты не зависят от времени. Рассмотрим два бесконечно близких события, происходящих в одной и той же точке пространства. Тогда интервал между этими событиями ds, как инвариантная величина, независимая от координат, определяет промежуток собственного (или истинного ) времени dτ следующим образом: ds 2 = c 2 dτ 2. Поскольку мы рассматриваем одну и ту же точку пространства, то пространственная часть не дает вклада в интервал, dx 1= dx 2= dx 3= 0. Поэтому от всего выражения интервала остается только часть: ds 2 = g 00 c 2 dt 2. Таким образом, истинное время в данной точке определяется через координатное формулой dτ = ( g 00) 1/2 dt . Если в данной точке g 00= 1, то истинное время совпадает с координатным. Поясним это. В зависимости от модели и исследуемых проблем, координатное время можно менять так же, как и пространственные координаты. А истинное время неизменно, поскольку оно однозначно определятся интервалом – инвариантной величиной.