Александр Петров - Гравитация. От хрустальных сфер до кротовых нор

В результате для h ab получим точно такие же волновые уравнения, как уравнения Максвелла для электрического поля или магнитной индукции. Причем уравнения показывают, что волна возмущений h ab также распространяется со скоростью света в плоском пространстве-времени.

Какой же физический смысл распространяющейся волны h ab ? Еще раз напомним, что метрика определяет способ измерения расстояний в пространстве-времени. Следовательно, величины h ab должны определять насколько и как этот способ будет возмущен. Образно можно представить себе гравитационную волну как мелкую «рябь», бегущую «по плоскости» пространства Минковского. Аналогично, метрические бегущие возмущения можно рассмотреть по отношению к какому-либо известному (фиксированному) искривленному пространству-времени. Например, если распространяющиеся возмущения рассматривают по отношению к космологическим решениям, то это гравитационные волны во Вселенной. Здесь уместно сравнение с мелкой «рябью» на поверхности океана, причем большой радиус кривизны мирового океана можно сравнить с фоновой кривизной пространства-времени Вселенной.

Легко понять, как гравитационные волны действуют на частицы и материю вообще. Их взаимодействие с макроскопическими телами можно сравнить с качанием «лодки» на ряби «фонового океана». Подобно тому, как заряженная частица в поле электромагнитной волны начинает совершать колебания, взаимодействие гравитационной волны с макроскопическими телами приводит к их движению. Появляются относительные ускорения между телами, и это приводит к изменению физического расстояния между ними.

В общем случае, в силу симметрии по индексам, метрическое возмущение h ab представляет 10 независимых компонент (величин). Какой физический смысл имеют эти величины, и все ли они имеют физическое (наблюдаемое) значение? Вспомним, что уравнения ОТО допускают изменения координат. При этом выбор различных систем координат не сказывается на физических эффектах, но может значительно упростить выражения. Воспользуемся этой свободой. В случае слабой плоской гравитационной волны, которую мы и рассматриваем, это позволяет наложить 8 условий на h ab , обращая 8 компонент из 10-ти в нуль.

Таким образом избавляются от так называемых нефизических степеней свободы. Оставшиеся две компоненты, для которых приняты обозначения h +и h ×, уже невозможно уничтожить никакими координатными преобразованиями, они описывают реальное воздействие гравитационной волны на пробные частицы. Их называют физическими степенями свободы.

Итак, гравитационная волна в ОТО имеет две степени свободы (поляризации). Как и электромагнитная, она является поперечной. Ее действие описывается следующим образом. В плоскости, перпендикулярной распространению, расположим по окружности пробные массивные частицы, как на рис. 10.2. Под действием одной из поляризаций волны окружность будет деформироваться в пульсирующий эллипс, большая и малая оси которого будут поочередно переходить одна в другую. Для другой поляризации ось соответствующего эллипса расположена под углом 45º к оси первого эллипса. В общем случае действием волны будет суперпозиция этих двух смещений.

Относительное изменение расстояния между двумя пробными частицами в поле плоской гравитационной волны определяется выражением ∆ l/l ≈ h /2. Это соотношение показывает, что по своему физическому смыслу амплитуда является безразмерной величиной. Часто ее называют «безразмерной амплитудой возмущений метрики», создаваемых гравитационной волной. Кроме того, важен угол между направлением распространения волны и отрезком, соединяющим частицы. В силу поперечного характера, если эти направления совпадают (угол нулевой), то эффекта не будет, если они ортогональны, то эффект максимален.

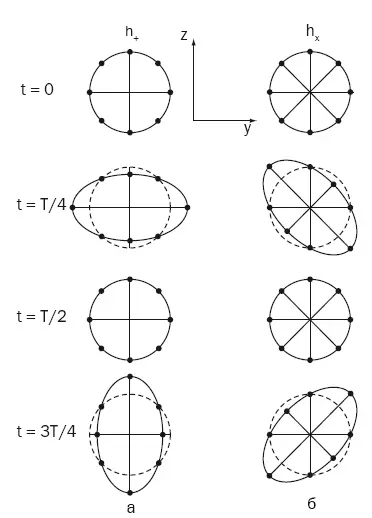
Рис. 10.2. Действие гравитационной волны

Гравитационное излучение чрезвычайно слабое. Это связано со слабостью гравитационного взаимодействия в природе. Например, электромагнитная константа связи (ее называют постоянной тонкой структуры) α= e 2/h c ≈ 1/137, где используются заряд электрона, постоянная Планка и скорость света. В то же время аналогичная безразмерная константа связи гравитационного взаимодействия имеет порядок α G = Gm p 2/h c = ( m p/ m Pl) 2 ≈ 10 –38, где используются масса протона и планковская масса. В отличие от электромагнитного излучения, когда каждый атом может излучить фотон, и его можно зарегистрировать, гравитационное излучение формируется большим количеством атомов, электронов и т. д. и становится существенным при несимметричном движении больших масс вещества (отдельных объектов) в целом.

Продолжая сравнение с электродинамикой, вспомним, что электромагнитное излучение генерируется переменным дипольным моментом. А при каких условиях возникает гравитационное излучение? Чтобы ответить на этот вопрос, объясним, что такое дипольный момент и моменты других порядков массивного тела.

Вспомним, что потенциал точечной массы в теории Ньютона

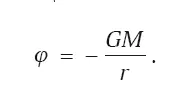
Если вместо точки взять сферическое тело (однородный шар) той же массы M с центром, где раньше была точка, то значение потенциала вне тела не изменится.

При несферичности рассматриваемого тела выражение для потенциала изменится, и изменения будут связаны непосредственно с отклонениями от сферичности. Величину отклонения можно представить так. Если сферическую составляющую принять за исходную симметрию, то первая степень отклонения (грубая) – дипольная, следующая (более «тонкая») – квадрупольная, и т. д. Тогда значение потенциала в выбранной точке можно представить в виде:

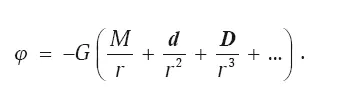
Здесь d – дипольный момент, а D – квадрупольный. Формула является символической: в ней не учтены коэффициенты, а также векторный и тензорный характер некоторых величин. Но она показывает, что при удалении от источника каждый из последующих членов ряда дает все меньший вклад в формирование потенциала.

В электродинамике излучение определяется изменением дипольнного момента (рис. 10.1) В гравитации дипольный момент, который является вектором, определяется следующим образом: из начала координат к каждому элементу массы Δ M проводится радиус-вектор R, после чего величины Δ M· R векторно суммируются по всем элементам массы. Ясно, что выбрав начало координат в центре масс, мы получим дипольный момент тождественно равный нулю. Это можно сделать всегда, поскольку в гравитации, в отличие от электромагнетизма, нет противоположных зарядов (нет отрицательных масс). Следовательно, не может быть и гравитационного излучения, связанного с дипольным моментом.