Ашот Григорьян - Механика от античности до наших дней

Заметим, что работа Эйлера по упругости воздуха привлекла внимание Ломоносова. Исследуя свойства селитры, Ломоносов, естественно, встретился с вопросом об упругой силе пороха и в этой связи писал 5 июля 1748 г. Эйлеру: «Я читаю с большой пользой для себя «Артиллерию» Робинса, снабженную Вами превосходными замечаниями» {167} 167 М. В. Ломоносов. Труды по физике и химии (1747—1752), т. 2. М.—Л., 1951, стр. 171—173. . Далее Ломоносов говорил о разработке им собственной теории упругости воздуха.

С задачами механики жидкостей Эйлер вновь встретился в 1749 г. при консультировании работ по проведению канала между Гавелем и Одером, а затем после изобретения Сегнером (1704—1777) гидравлической машины, известной теперь каждому школьнику под именем «Сегнерова колеса». Анализу устройства и действия этой машины и попыткам ее практического применения посвящена обширная переписка между Эйлером и Сегнером за 1750— 1754 гг. {168} 168 См. Н. М. Раскин. Вопросы техники у Эйлера. — В кн.: Леонард Эйлер. Сборник статей в честь 250-летия со дня рождения, представленных Академии наук СССР, стр. 509—536. и ряд их статей. Эйлер внес в первоначальный вариант машины Сегнера столь важные усовершенствования (присоединение так называемого направляющего аппарата и др.), что именно машина Эйлера, а не Сегнера является прообразом реактивных гидравлических турбин, строить которые начали три четверти века спустя. Вместе с тем в работе «Более полная теория машин, проводимых в движение реакцией воды», напечатанной в 1754 г. в 10-м томе «Мемуаров Берлинской академии наук», Эйлер впервые разработал общую теорию движения несжимаемой идеальной жидкости в узких трубах двоякой кривизны, вращающихся около неподвижной оси. При этом он фактически оперировал с понятием ускорения Кориолиса, которое французский механик ввел в 1831 г.

Методы расчета гидравлических турбин Эйлера, покоящихся на струнной теории, сохранили с соответствующими улучшениями свое значение в практическом машиностроении. Известный немецкий специалист по прикладной математике профессор К. Шредер пишет: «Можно сказать, что эти выдающиеся работы характеризуют Эйлера как ученого-инженера в современном смысле слова» {169} 169 К. Шредер. О трудах Леонарда Эйлера в области прикладных наук. — В кн.: Леонард Эйлер. Сборник статей в честь 250-летия…, стр. 38. .

В 50-е годы Эйлер подготовил несколько больших работ по гидромеханике. Первая из них «Начала движения жидкостей» была напечатана в VI томе «Novi Commen-tarii» за 1756—1757 гг. В ней излагались общие начала гидро- и аэростатики, выводилось уравнение неразрывности для жидкости с постоянной плотностью. Значительная часть материала этой статьи нашла свое отражение в других работах Эйлера, написанных позднее, но вышедших раньше. Это были следующие три работы Эйлера: «Общие начала состояния равновесия жидкостей», «Общие начала движения жидкостей» и «Продолжение исследований по теории движения жидкостей», напечатанные в 1753—1755 гг. во 2-м томе «Мемуаров Берлинской академии наук». Эти классические работы составили основополагающий трактат по гидродинамике.

Первая из этих трех работ содержит глубокий анализ понятия давления, его свойств и приложений, а также вывод дифференциального условия равновесия жидкостей и газов.

Вторая статья имела решающее значение для всего последующего развития гидро- и аэродинамики, ибо именно в ней был впервые опубликован вывод уравнения неразрывности для сжимаемой жидкости и общих уравнений гидродинамики, называемых теперь уравнениями Эйлера.

В третьей статье приведены некоторые теоремы о движении жидкостей и газов в узких трубках произвольной формы.

Из других гидродинамических работ Эйлера упомянем еще ряд статей о распространении звука, о малых колебаниях воздуха в трубах постоянного и переменного сечения с применениями к теории музыки и т. д. Эти работы переплетались с аналогичными исследованиями Д. Бернулли. Математическим аппаратом этих исследований являются уравнения в частных производных второго и высшего порядков, большей частью линейные. Именно той ролью, которую играют уравнения в частных производных в гидромеханике, а также в математической физике, определялся глубокий интерес Эйлера к этой новой тогда отрасли анализа. Эйлер выработал целый ряд приемов интегрирования различных уравнений в частных производных и впервые ввел в рассмотрение некоторые их типы. Мы упомянем здесь лишь весьма важное в газовой динамике и дифференциальной геометрии уравнение

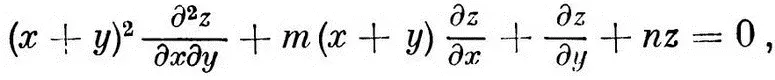
впервые изученное Эйлером, а затем С. Пуассоном (1781-1840), Б. Риманом (1826-1866), Ж.-Г. Дарбу (1842-1917). В настоящее время это уравнение встречается, в частности, в задачах о движениях газа с околозвуковыми или сверхзвуковыми скоростями.

Еще в древности были установлены некоторые эмпирические правила, соблюдение которых обеспечивало прочность и надежность сооружений. В XIII в. Иордан Неморарий предпринял первую попытку определить форму кривой, которую принимает под действием нагрузки ось закрепленного стержня, т. е. упругой линии. В XVI в. Леонардо да Винчи изучал вопрос о сопротивлении балок изгибу; он занимался, вероятно, и задачей о сопротивлении колонн. Галилей в «Беседах и математических доказательствах, касающихся двух новых наук» (1638) положил начало учению о сопротивлении материалов. В 1678 г. Гук нашел основной закон линейной зависимости между силой и деформацией при растяжении пружин, струн, тонких стержней и произвел ряд соответствующих опытов. Так были заложены основы теории упругости {170} 170 Подробнее— С. П. Тимошенко. История науки о сопротивлении материалов с краткими сведениями из истории теории упругости и теории сооружений. М., Физматгиз, 1957, стр. 9—36. .

В 1691 г. Я. Бернулли начал серию исследований, посвященных проблеме упругой линии. Некоторые предпосылки и выводы его неточны, но в целом он значительно продвинулся вперед. В частности, он вывел дифференциальное уравнение задачи и доказал, что кривизна линии изгиба пропорциональна изгибающему моменту в точке, — положение, которое использовали затем другие ученые, и среди них Эйлер.

Эйлер рассмотрел задачу об упругих кривых в большом приложении к «Методу нахождения кривых линий» (1744); в русском переводе оно занимает 125 страниц. Работа эта была вызвана замечанием, сделанным Д. Бернулли в письме Эйлеру от 22 октября 1742 г. Бернулли предложил применить к задаче изопериметрический метод, т. е. свести ее к задаче о минимуме некоторого интеграла. Реализуя эту идею, Эйлер по-новому вывел дифференциальное уравнение Я. Бернулли и решил его при различных граничных условиях. В другом отделе того же приложения Эйлер рассмотрел продольный изгиб колонны под действием осевой сжимающей силы и получил выражение для предельной нагрузки, превышение которой приводит к изгибу; эта формула имеется теперь во всех справочниках. Затем Эйлер переходит к изучению колебаний стержней, начиная со стержня, в естественном состоянии прямого и с жестко заделанным в вертикальном положении верхним концом. Эта задача приводится к интегрированию обыкновенного линейного однородного дифференциального уравнения четвертого порядка. В заключение разобраны задачи о колебании стержней при других предположениях о закреплении их концов.