Майкл Файер - Абсолютный минимум. Как квантовая теория объясняет наш мир

Форма спектра, изображённого на рис. 9.1, почти совпадает с реальным солнечным спектром. Расчётный спектр получен путём подгонки температуры в формуле Планка до наилучшего соответствия экспериментальному спектру. Температура, которая даёт такое соответствие, составляет 5780 K, где K — кельвины. Кельвин — это единица температуры по абсолютной шкале, разработанной Уильямом Томсоном, первым бароном Кельвином (лорд Кельвин, 1724–1907). Шкала Кельвина используется в физике и химии, поскольку нулевая отметка на этой шкале (0 K) имеет чётко определённый физический смысл. При 0 K прекращаются все движения атомов, связанные с кинетической энергией, то есть с теплом, с энергией движения частиц. Чтобы получить температуру в градусах Цельсия (°C), следует из температуры в кельвинах вычесть 273. Таким образом, по шкале Цельсия температура Солнца составляет 5507 °C.

Поразительно, что формула Планка, выведенная с опорой на первую квантовую идею о том, что энергия электронов, «осциллирующих» в металле, не является непрерывной, оказалась применимой к температуре звёзд. Расчётный спектр, изображённый на рис. 9.1, является непрерывным, поскольку горячий объект порождает непрерывное распределение цветов (энергии квантов света). Хотя экспериментальные данные в целом соответствуют кривой на рис. 9.1, на них также совершенно отчётливо проявляются детали, которые отсутствуют на черноте́льном спектре Солнца. На рис. 9.2 изображён солнечный спектр с тёмными линиями, отражающими нехватку света некоторых частот. Спектр, изображённый на рис. 9.1, соответствует излучению, испускаемому Солнцем. Тёмные линии — это узкие диапазоны длин волн, которые не доходят до Земли. Они называются линиями, или полосами, поглощения. Те же самые линии совершенно отчётливо видны в спектрах света, приходящего от других звёзд.

Длины волн, соответствующие тёмным линиям в солнечном спектре, можно наблюдать как отдельные цвета дуговой лампы, заполненной водородом. Водородная дуговая, или газоразрядная, лампа представляет собой заполненный водородом герметичный стеклянный цилиндр с электродами на концах. Когда достаточно высокий положительный электрический потенциал подаётся на один электрод, а отрицательный — на другой, в лампе возникает электрическая дуга, подобная маленькой непрерывно бьющей молнии. Цвета, или длины волн, в диапазоне видимого света, испускаемые лампой, соответствуют длинам волн тёмных линий спектра на рис. 9.2.

Рис. 9.2. Видимая часть солнечного спектра. Непрерывная последовательность цветов — это черноте́льный спектр. Тёмные линии, или полосы, — это цвета, соответствующие длинам волн, которые не доходят до Земли, так что они выглядят отсутствующими цветами в солнечном спектре. Длины волн этих линий отложены на шкале вдоль спектра в нанометрах (1 нм = 10 −9 м)

Первая попытка объяснить линейчатый спектр водорода в видимом диапазоне была предпринята в 1885 году школьным учителем и математиком Иоганном Бальмером (1825–1898). Бальмер заметил, что частоты f этих линий в видимой части спектра можно описать формулой

f ~(1/2 2)−(1/ n 2).

Символ ~ означает пропорциональность, то есть указывает на наличие постоянного множителя, о котором говорится ниже. В этом уравнении n — целое число больше 2, то есть 3, 4, 5 и т. д.

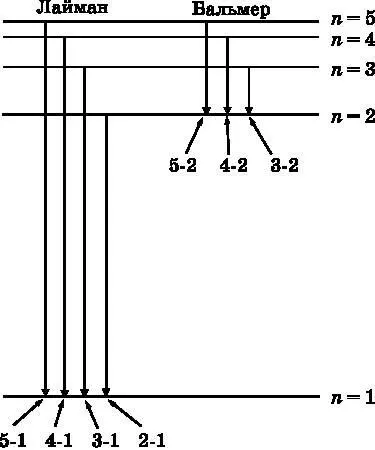
Эти линии в видимой части спектра называются бальмеровской серией. Позднее были открыты линии в ультрафиолетовой и инфракрасной частях спектра. Их назвали сериями Лаймана и Пашена соответственно в честь их первооткрывателей — американского физика и спектроскописта Теодора Лаймана (1874–1954) и немецкого физика Луиса Карла Генриха Фридриха Пашена (1865–1947). В 1888 году шведский физик и спектроскопист Йоханнес Ридберг (1854–1919) опубликовал формулу, которая описывала все спектральные линии, видимые в излучении водородной дуговой лампы и в спектрах поглощения солнечного и звёздного света. Формула Ридберга для частоты спектральных линий водорода имеет вид

f = R H∙[(1/ n 1 2)−(1/ n 2 2)],

где n 1— целые числа, начиная с 1, а n 2— другие целые числа, которые должны быть больше n 1. Значение n 1=1 даёт лаймановскую серию, n 1=2 — бальмеровскую, n 1=3 — серию Пашена.

Константа R Hназывается постоянной Ридберга для атома водорода. Её значение составляет R H=109677,6 см −1и выражено числом волн ( см −1). При использовании этого значения в формуле Ридберга частоты спектральных линий, определяемые целыми числами n 1и n 2, выражаются волновыми числами. Для перевода результата в герцы надо умножить полученное значение на скорость света, то есть на 3∙10 10 см / сек . Чтобы найти длину волны спектральной линии, надо взять величину, обратную частоте, выраженной числом волн, то есть разделить единицу на частоту, выраженную числом волн. Например, если n 1=2, а n 2=3, то

f = R H∙[(1/2 2)−(1/3 2)] = R H∙[(1/4)−(1/9)] = 1,52∙10 4 см −1

представляет собой частоту, выраженную числом волн. Обратная величина для этого числа составляет 6,56∙10 −5 см = 656∙10 −9 м = = 656 нм . Таким образом, длина волны составляет 656 нм — это красная линия в серии Бальмера, изображённой на рис. 9.2.

При обсуждении рис. 8.7 уже говорилось о дискретности оптических переходов между квантовыми энергетическими уровнями для частицы в ящике. На рис. 8.7 показаны переходы между состояниями частицы в ящике, при которых n =1 превращается в n =2 и n =1 превращается в n =3. В связи с этим не должен стать большим сюрпризом тот факт, что оптические переходы в атоме водорода могут соответствовать дискретному набору частот, которые зависят от целых чисел. Однако в 1888 году, когда была получена формула Ридберга, оставалось ещё 12 лет до появления идеи квантования энергетических уровней, с помощью которой Планк объяснил черноте́льное излучение, и 37 лет до того, как в 1925 году сформировалась полноценная квантовая теория. Различные серии спектральных линий, энергии которых связаны посредством целых чисел по формуле Ридберга, можно понять как оптические переходы между дискретными энергетическими уровнями, связанные с атомом водорода.