Майкл Файер - Абсолютный минимум. Как квантовая теория объясняет наш мир

Энергии различных состояний атома водорода описываются единственным квантовым числом n . Однако в действительности есть четыре квантовых числа, связанных с электронами в атомах. Они появляются при решении задачи об атоме водорода в рамках квантовой теории. Одно из них существенно лишь для атомов и молекул, имеющих более одного электрона. В этом смысле атом водорода является частным случаем, поскольку в нём всего один электрон. Для атома водорода, помимо главного квантового числа n , есть ещё два квантовых числа — l и m . Число l называется орбитальным квантовым числом, m — магнитным квантовым числом. От них в сочетании с квантовым числом n зависит, сколько различных состояний связано с конкретным значением энергии, они также определяют форму волновых функций. Четвёртое квантовое число обозначается s . Его называют спи́новым квантовым числом.

Когда Бор решал задачу об атоме водорода, в рамках старой квантовой теории считалось, что электрон движется по орбитам, имеющим разные формы и значения энергии. Корректное квантовое решение Шрёдингера для атома водорода даёт энергетические уровни и волновые функции, которые соответствуют боровским орбитам и называются «орбиталями». Обсуждая атомы и молекулы, мы часто используем термины «волновая функция» и «орбиталь» в качестве синонимов. Орбитали являются волнами амплитуды вероятности, которые подчиняются принципу неопределённости Гейзенберга, чем отличаются от боровских орбит.

Как уже отмечалось выше, главное квантовое число n может принимать целочисленные значения n ≥1, то есть 1, 2, 3, 4 и так далее, а l может принимать значения от 0 до n −1 с целым шагом. Число m может иметь значения от l до − l с целым шагом. Наконец, число s может принимать только два значения: +½ и −½. Сводка возможных значений квантовых чисел приведена в таблице ниже.

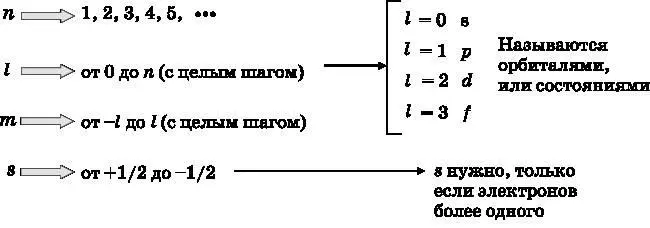
По историческим причинам состояния с различными значениями квантового числа l имеют индивидуальные обозначения. Состояние l =0 называется s -орбиталью. При l =1 говорят о p -орбитали, при l =2 — это d -орбиталь, а при l =3 — f -орбиталь. Для обсуждения всех атомов нам не понадобится заходить далее f -орбиталей, то есть l =3. Как показано ниже, различные орбитали имеют разные формы.

Поскольку энергии состояний (орбиталей) атома водорода зависят только от квантового числа n , для n >1 имеется более одного состояния с одинаковой энергией. Для n =1 имеем l =0 и m =0 (см. таблицу), поэтому существует единственная орбиталь с n =1. Для этой орбитали l =0, так что её обозначают как 1 s -орбиталь. Для n =2 число l может быть равно 0, что даёт 2s-орбиталь. Однако для n =2 число l также может равняться 1. При l =1 число m может быть равно 1, 0 или −1 (см. таблицу). При l =1 — это p -орбиталь, причём существуют три разные p -орбитали, обозначаемые 2 p 1, 2 p 0и 2 p −1. Здесь 2 — это главное квантовое число n, p означает l =1, а три индекса— это три возможных значения m . Таким образом, для n =2 существует четыре различных состояния.

Если n =3, то l может быть равно нулю, что даёт 3 s -орбиталь. Также l может быть равно 1, что при m = 1, 0 и −1 даёт орбитали 3 p 1, 3 p 0, и 3 p −1. Кроме того, l может быть равно 2. Для l =2 число m может иметь значения 2, 1, 0, −1 и −2. Это d -орбитали: 3 d 2, 3 d 1, 3 d 0, 3 d −1и 3 d −2. Всего имеется пять d -орбиталей. Таким образом, для n =3 имеется девять различных состояний: одна s -орбиталь, три p -орбитали и пять d -орбиталей. Когда n =4, есть 4 s -орбиталь, три различные 4 p -орбитали (4 p 1, 4 p 0и 4 p −1), пять различных 4 d -орбиталей (4 d 2, 4 d 1, 4 d 0, 4 d −1и 4 d −2). Дополнительно имеется семь f -орбиталей: 4 f 3, 4 f 2, 4 f 1, 4 f 0, 4 f −1, 4 f −2и 4 f −3. Таким образом, для n =4 имеется в общей сложности 16 состояний: одна s -орбиталь, три p -орбитали, пять d -орбиталей и семь f -орбиталей.

Как уже говорилось, каждая из этих орбиталей имеет свою форму. Довольно часто орбитали называют в соответствии с их формой. Например, три различных 2 p -орбитали, вместо того чтобы обозначать их 2 p 1, 2 p 0и 2 p −1, называют 2 p x, 2 p zи 2 p y. Связь между этими индексами и формами прояснится, когда мы познакомимся с соответствующими формами.

На рис. 10.1 представлена диаграмма энергетических уровней атома водорода. Изображены уровни с n от 1 до 5. Для удобства восприятия масштаб интервалов не соблюдается, но, как и показано, с увеличением n интервал между уровнями становится меньше. Также с увеличением n возрастает число различных состояний (орбиталей), соответствующих конкретному значению n . Водород — это особый случай, поскольку у него имеется лишь один электрон. Для водорода все орбитали с одинаковым значением n обладают равной энергией. В следующей главе будет объяснено, что в атомах с несколькими электронами орбитали с разными значениями l при одном и том же n обладают разными энергиями.

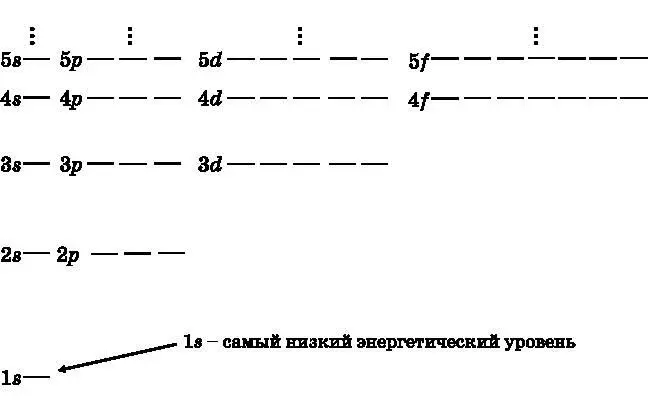
Рис. 10.1. Диаграмма энергетических уровней водорода. Изображены первые пять энергетических уровней. Для удобства восприятия масштаб интервалов между уровнями не соблюдается. Энергия зависит только от главного квантового числа n. Показано количество орбиталей каждого типа. При n = 4 имеется одна s-орбиталь, три разные p-орбитали, пять разных d-орбиталей и семь разных f-орбиталей {13} 13 На уровне n =5 не показаны девять g -орбиталей, соответствующих l =4. — Примеч. пер. . Диаграмму можно продолжить для n = 6. Различные уровни иногда называют оболочками