Майкл Файер - Абсолютный минимум. Как квантовая теория объясняет наш мир

Хотя значения энергии в атоме водорода зависят только от главного квантового числа n , квантовые числа l и m тоже играют важную роль. Они определяют форму орбиталей и другие свойства, присущие атому водорода. Например, квантовое число m называется магнитным квантовым числом. Три 2 p -орбитали (2 p 1, 2 p 0и 2 p −1) различаются значениями квантового числа m . Когда атом водорода помещают в магнитное поле, энергии этих трёх орбиталей перестают быть одинаковыми.

Из диаграммы энергетических уровней, вычисленных с помощью уравнения Шрёдингера (см. рис. 10.1), становится ясно, как возникает эмпирическая диаграмма, представленная на рис. 9.3. Оптические переходы, видимые как линии в спектре атома водорода и описываемые формулой Ридберга, — это переходы между энергетическими уровнями атома водорода, энергии которых вычисляются на основе квантовой теории без каких-либо подгоночных параметров.

Как уже упоминалось, квантовые числа n, l и m вместе определяют формы волновых функций. Для s -орбиталей l =0. Это означает, что электрон не имеет углового момента {14} 14 Квантовое число l называется орбитальным и характеризует момент импульса электрона, называемый также угловым моментом. — Примеч. пер. в своём движении относительно ядра атома. Все направления выглядят равноценными, так что s -орбитали — это сферически симметричные трёхмерные волны амплитуды вероятности. На рис. 10.2 схематически показаны орбитали (волны амплитуды вероятности) 1 s , 2 s и 3 s . Более тёмный тон означает бо́льшую вероятность обнаружить электрон на соответствующем расстоянии от центра. Расстояния, на которых вероятности достигают максимума, показаны сплошными окружностями. Середины белых областей внутри орбиталей 2 s и 3 s (пунктирные окружности) — это узлы, то есть области, где вероятность обнаружить электрон обращается в нуль. При переходе от 1 s к 2 s и 3 s размеры орбиталей значительно возрастают. С увеличением квантового числа n повышается вероятность обнаружить электрон вдали от ядра.

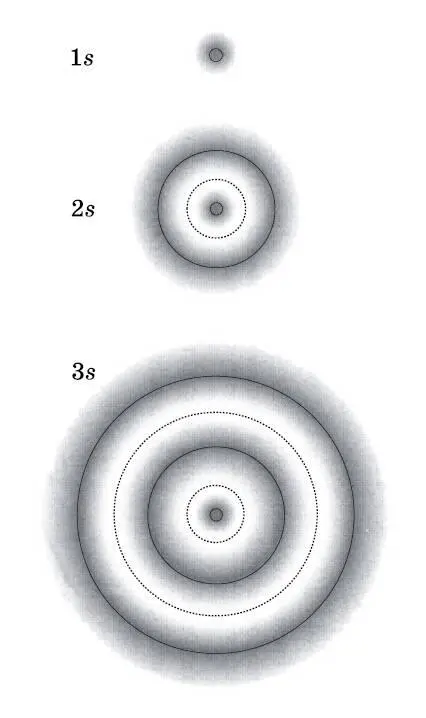
Рис. 10.2. Двумерные представления орбиталей 1 s, 2 s и 3 s. В действительности они сферические. Более тёмный тон соответствует более высокой вероятности обнаружения электрона. Сплошными окружностями обозначены максимальные значения этой вероятности. Пунктирные окружности — это узлы, где данная вероятность обращается в нуль. При данном способе изображения орбитали имеют довольно чёткую внешнюю границу. Орбитали — это волны, которые становятся очень малыми на больших расстояниях, но обращаются в нуль лишь тогда, когда расстояние от центра стремится к бесконечности

Увеличение размера орбиталей — одна из причин того, что энергия возрастает с увеличением квантового числа n . Формула для энергетических уровней атома водорода начинается со знака «минус»: E n= − R H/ n 2. Принято считать, что более низкая энергия — это бо́льшая по абсолютной величине отрицательная энергия. Атом водорода состоит из протона и электрона, притягивающихся друг к другу в результате кулоновского, то есть электростатического, взаимодействия. Противоположные заряды притягиваются. Протон — это положительно заряженная частица, а электрон заряжен отрицательно. Когда протон и электрон разнесены бесконечно далеко, они не ощущают влияния друг друга. Взаимодействия между ними из-за большого расстояния нет. Система имеет нулевую энергию, когда её частицы разнесены на бесконечно большое расстояние.

Взаимодействие электрона и протона усиливается по мере того, как они сближаются. Энергия системы убывает, становясь всё более отрицательной. На орбитали 2 s электрон в среднем находится дальше от протона, чем на орбитали 1 s , на орбитали 3 s электрон в среднем ещё дальше от протона. Это видно на рис. 10.2. С увеличением квантового числа энергия выражается всё меньшими отрицательными числами. При больших значениях n требуется меньше энергии, чтобы разделить электрон и протон, то есть ионизировать атом. Ионизация — это процесс отрыва электрона от атома, так что они более не связаны друг с другом. При n =1 для ионизации атома требуется энергия R H. Её нужно передать атому, чтобы превзойти энергию связи, равную — R H. При n =2 энергия, требуемая для ионизации атома водорода, составляет всего R H/4, а при n =3 необходимая энергия ещё меньше и составляет R H/9.

Чтобы лучше представить себе пространственное распределение вероятности обнаружить электрон в определённом положении, полезно построить для волновых функций два типа графиков. Один из них — это просто график волновой функции в зависимости от расстояния до ядра. Это полезный график, но кое в чём он вводит в заблуждение. Второй тип графика называют радиальным распределением функции, и мы вкратце его опишем.

На рис. 10.3 представлен график волновой функции Ψ( r ) в зависимости от расстояния до протона, который находится в центре атома. График этого типа показывает амплитуду вероятности обнаружить электрон вдоль одной прямой линии, уходящей радиально от центра. Значение r отсчитывается от тёмного центра распределения электрона на рис. 10.2 вправо в горизонтальном направлении. На рис. 10.3 видно, что вероятность обнаружить электрон быстро убывает вдоль отдельно взятой прямой и приближается к нулю, когда расстояние от ядра достигает 3 Å.

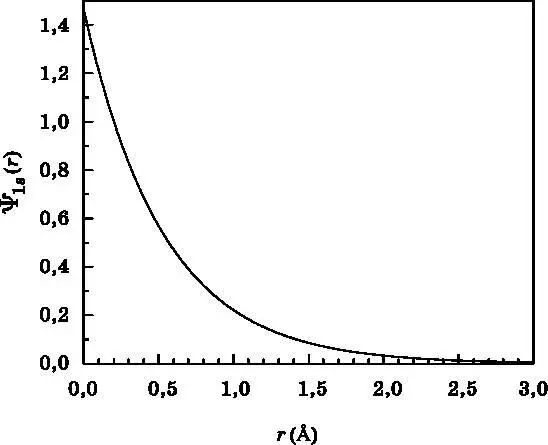
Рис. 10.3. График волновой функции Ψ( r ) для орбиталей 1s в зависимости от расстояния rдо протона. Значение Ψ( r ) пропорционально вероятности обнаружить электрон вдоль линии, радиально уходящей от центра атома. Расстояние rвыражено в ангстремах (1 Å = 10 −10 м)

Проблема с графиком того типа, который представлен на рис. 10.3, состоит в том, что он не учитывает трёхмерную природу атома. Рассматривая 1 s -орбиталь на рис. 10.2, мы понимаем, что можно обнаружить электрон на некотором расстоянии от центра, двигаясь не только вдоль линии, направленной вправо, но и вдоль линии, направленной влево, вверх или вниз. Можно также сдвинуться в любом диагональном направлении на расстояние r и получить ту же самую вероятность обнаружить электрон. Поскольку атом трёхмерен, можно также выйти из плоскости страницы и тоже обнаружить электрон. Если нужно знать вероятность обнаружения электрона на определённом расстоянии r от протона, то следует произвести суммирование по всем таким радиальным направлениям.