Майкл Файер - Абсолютный минимум. Как квантовая теория объясняет наш мир

Как уже подробно говорилось, волновые функции — это волны амплитуды вероятности. Подобно другим волнам, они могут быть положительными и отрицательными. В нижней части рис. 10.5 показана функция радиального распределения для состояния 2 s . Это вероятность обнаружить данный электрон на расстоянии r от ядра. Вероятности всегда имеют положительные значения, поскольку являются квадратами волновой функции, которые всегда положительны.

Волна может быть положительной или отрицательной, но имеющие смысл значения вероятности являются положительными числами или нулём. Функция радиального распределения показывает, что бо́льшая часть вероятности приходится на интервал от 2 до 4 Å; это также видно на рис. 10.2, но без количественного описания. Пик вероятности приходится на отметку приблизительно 2,8 Å.

Из рис. 10.6 видно, что волновая функция 3 s -орбитали имеет два узла, то есть дважды пересекает ноль. В этом отношении волновые функции атома водорода подобны волновым функциям частицы в ящике (см. рис. 8.4). При n =1 узлов нет. При n =2 имеется узел. При n =3 имеется два узла. Число узлов для s -орбиталей равно n −1. Волновая функция 3 s начинается с положительного значения, затем становится отрицательной, а потом вновь положительной. В конце концов она спадает до нуля, становясь очень малой за отметкой 16 Å. Функция радиального распределения для 3 s -орбитали показывает, что область наибольшей вероятности обнаружить электрон находится относительно далеко от ядра. Пик вероятности расположен приблизительно на 7 Å, а на интервал от 5 до 11 Å приходится наибольшая вероятность найти электрон. Три функции радиального распределения, изображённые на рис. 10.4–10.6, дают количественное выражение для информации, схематически представленной на рис. 10.2. По мере увеличения главного квантового числа ( n ) s -орбитали становятся больше и количество узлов возрастает.

Для 2 s -орбитали n =2, l =0 и m =0. Однако при n =2 число l также может быть равно 1 и с ним могут быть связаны три значения m : m = 1, 0, −1. Эти три значения m соответствуют трём различным 2 p -орбиталям. Они показаны на диаграмме энергетических уровней на рис. 10.1.

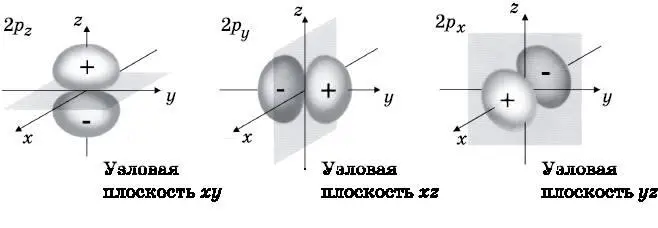
Рис. 10.7. Схематическое изображение трёх 2p-орбиталей атома водорода: 2p z , 2p y и 2p x . У каждой из них имеется два лепестка: один положительный и один отрицательный. У каждой есть узловая плоскость, то есть плоскость, где вероятность обнаружить электрон равна нулю. Лепестки 2p z -орбитали располагаются вдоль оси z, а узловой является плоскость xy, выделенная серым тоном. У 2p y -орбитали лепестки расположены вдоль оси y, а основная плоскость — в плоскости xz. Лепестки 2p x -орбитали лежат вдоль оси z, а узловая плоскость — это yz. Лепестки на этой схеме показывают, где находится область с максимальной амплитудой вероятности для электрона. Волны амплитуды вероятности плавно спадают к нулю вдали от ядра (протона), а не обрываются резко, как на этих диаграммах

Три разные 2 p -орбитали схематически представлены на рис. 10.7. Как уже говорилось, 2 p -орбитали с учётом их формы обычно обозначают 2 p z, 2 p yи 2 p x. Каждая из этих орбиталей имеет два лепестка — положительный и отрицательный. Какой лепесток считать положительным, а какой — отрицательным, не важно, но знак должен меняться, поскольку имеется узловая плоскость. Лепестки 2 p z-орбитали расположены вдоль оси z . Узловая плоскость (на рисунке показана серым тоном) — это плоскость xy ( z =0). Вероятность обнаружить электрон на этой плоскости равна нулю. Знак волновой функции меняется при переходе через узел. У 2 s -орбитали имеется радиальный узел. Это сферическая поверхность на определённом расстоянии от центра, представляющая собой узел. Каждая из p -орбиталей имеет узловую плоскость, то есть совокупность направлений (плоскость), где располагается узел. У 2 p -орбиталей нет радиального узла, но у 3 p -орбиталей в дополнение к узловой плоскости есть радиальный узел, а у 4 p -орбиталей имеется два радиальных узла и т. д.

Лепестки 2 p y-орбитали направлены вдоль оси y , а её узловая плоскость — это xy . У 2 p x-орбитали лепестки направлены вдоль оси x , а узловой является плоскость yz . Приведённые на рис. 10.7 схематические изображения 2 p -орбиталей подобны изображениям s -орбиталей на рис. 10.2. Рисунок 10.7 позволяет понять, в каких областях амплитуда вероятности для электрона велика. Однако важно понимать, что эти волны амплитуды вероятности плавно спадают с удалением от ядра. На рисунке лепестки обрываются резко, но волновые функции на больших расстояниях ведут себя подобно тому, как это показано на рис. 10.3 для 1 s -орбитали. Тем не менее рис. 10.7 полезен для того, чтобы представить себе формы 2 p -орбиталей. Эти формы окажутся очень важными, когда речь пойдёт о молекулярных связях и формах молекул.

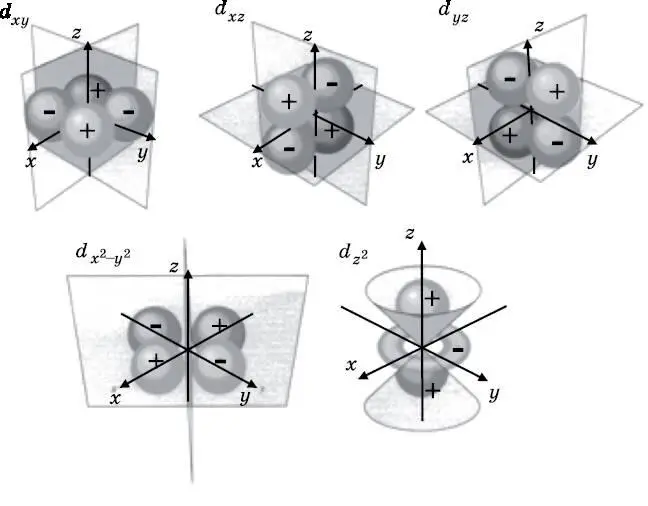
При n =3 число l может быть равно 0, что даёт 3 s -орбиталь. Также l может быть равно 1, что при m = 1, 0, −1 даёт три различные 3 p -орбитали. Кроме того, l может быть равно 2, что при m = 2, 1, 0, −1, −2 даёт пять различных 3 d -орбиталей. Они показаны на диаграмме энергетических уровней (см. рис 10.1). На рис. 10.8 изображено пять различных 3 d -орбиталей. Как и p -орбиталям, d -орбиталям часто дают названия, отражающие их форму, вместо того чтобы обозначать их квантовым числом m . Четыре из этих орбиталей имеют в целом одинаковую форму. У каждой имеется четыре лепестка и две узловые плоскости. Два из этих лепестков положительные, а другие два отрицательные. При пересечении узловой плоскости волновая функция меняет знак. Пятая орбиталь ( d x 2) имеет другую форму, но у неё по-прежнему две узловые поверхности. Это конические поверхности, изображённые на диаграмме. Как и в случае с p -орбиталями, на рис. 10.8 тоном выделены области с наибольшей амплитудой вероятности обнаружения электрона. Эти волны амплитуды вероятности спадают к нулю с увеличением расстояния от ядра.