Карлос Касадо - Вселенная работает как часы. Лаплас. Небесная механика.

Однако событие, вероятность которого мы хотим рассчитать, иногда может быть составным. В этом случае необходимо применить не правило Лапласа, а правило произведения, которое мы также находим у Лапласа: если для появления события А нужно, чтобы в одно и то же время произошли два других события, В и С, то вероятность события А равна произведению вероятности события В, умноженной на вероятность события С, при условии, что событие В уже произошло. Это формулу мы знаем сегодня как формулу условных вероятностей. Например, вероятность, что выпадет 6, если мы бросаем одну кость, равна 1 /6. Какова вероятность получить сразу две 6? На основании правила умножения необходимо умножить вероятность выпадения первой 6(1 /6) на вероятность выпадения второй 6 (также 1/6, поскольку эти два события не зависят друг от друга): 1/6 х 1/6 = (1/6)² = 1/36 (-2,8%).

Шевалье де Мере описывает следующую ситуацию: игроки А и В играют друг против друга, и каждый ставит 32 золотые монеты, то есть всего 64 монеты, которые заберет первый игрок, выигравший три партии. Однако они вынуждены прервать игру. Как следует разделить выигрыш, если один из них победил в двух партиях, а второй — только в одной? Ошибочное решение для этой задачи нашел Лука Пачоли в XV веке. Он предложил игрокам разделить деньги исходя из количества побед: так как они сыграли три партии и игрок А выиграл две из них, а игрок В — только одну, А должен забрать 2/3 денег, а В — 1/3. Однако Кардано доказал, что это неверное решение, потому что оно не учитывает количество партий, которое каждый игрок должен был выиграть, чтобы забрать весь банк.

Решение нашли Паскаль и Ферма — каждый своим способом. «Я вижу, — писал первый второму, — что истина одна и та же в Тулузе и Париже».

Предположим, что А и В в одинаковой степени ловки в игре (в каждой партии вероятность, что один выиграет у другого, равна 1/2); вероятность, что А выиграет третью партию у В, — 3/4, так как есть два возможных исхода: либо он выиграет с первой попытки (с вероятностью 1/2, финальный счет тогда 3:1), либо со второй (вероятность 1/2 х 1/2 = 1/4, финальный счет 3:2). Сумма вероятностей этих двух исходов — 3/4. Напротив, вероятность того, что В выиграет, — лишь 1/4, поскольку ему для этого необходимо выиграть два раза подряд (1/2 х 1/2 = 1/4). Таким образом, следует разделить монеты следующим образом: 3/4 для А (48 монет) и 1/4 — для В (16 монет). Впоследствии Лаплас обобщает эту задачу исходя из гипотезы, что два игрока играют по-разному.

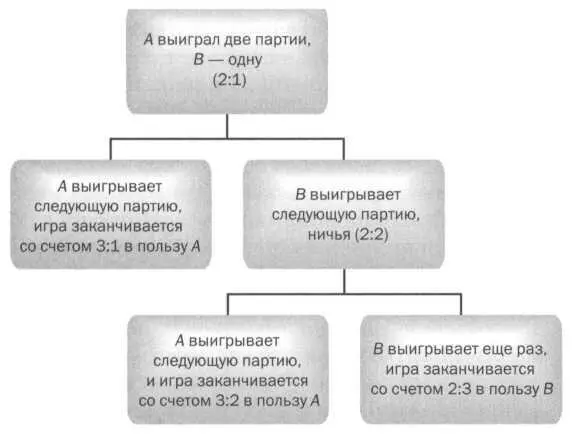
Схема различных возможностей завершить игру.

Первая публикация этого позднего труда — Лапласу было уже 62 года — состоялась в 1782 году. Работа была посвящена Наполеону. Автор подчеркивал, что расчет вероятностей применялся «к самым важным жизненным вопросам, которые по большей части являются лишь задачами вероятности». Наполеон в ответ назвал теорию вероятностей «первой из наук». Лаплас в течение десятилетий полностью посвятил себя небесной механике, но потом он вновь взялся за свои прежние труды о вероятностях и отправил в издательство научный трактат на эту тему.

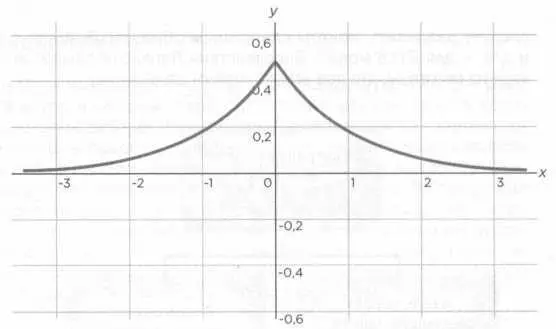
РИС.1

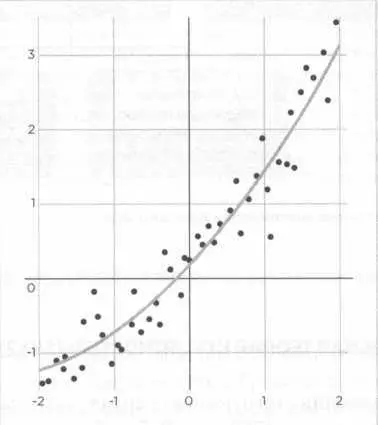
РИС. 2

Как гласило название, Лаплас стремился предложить аналитическую теорию вероятностей, то есть установить связь между анализом и расчетом вероятностей — двумя дисциплинами, тогда еще полностью разделенными.

Важен тот факт, что в своей книге Лаплас исследовал центральную предельную теорему, имеющую решающее значение для статистики и теории вероятностей. В своем труде от 1773 года он изучал увлекательный вопрос, связанный с определением реального положения звезды на основании серии наблюдений. Здесь недостаточно применить арифметический метод, ведь необходимо доказать, что выбранное значение минимизирует погрешность, то есть разницу между реальным и наблюдаемым явлениями. Лаплас интерпретировал эту проблему, рассматривая фактическое положение звезды в качестве причины наблюдаемых положений, и предположил, что погрешности зависят от случая. Искусно используя теорему Байеса, ученый пришел к выводу, что возможно начертить кривую, которая представляла бы распределение погрешностей вокруг истинного значения. Кривая является симметричной и нисходящей, исходит из центрального значения; чем больше мы удаляемся от этой точки, тем больше вероятность, что мы допускаем погрешность измерения. Чем ближе мы к вершине кривой, тем больше вероятность того, что мы ближе к фактическому значению. Решая дифференциальное уравнение, Лаплас сделал вывод, что кривая распределения погрешностей (рисунок 1, страница 136) выражается экспоненциальной функцией:

φ(x) = (e-|x|)/2.

Лаплас не первый определил нормальное распределение, равно как и экспоненциальную функцию (хотя и выраженную с помощью другой формулы). Она была введена Муавром в начале XVIII века. Обычная кривая распределения погрешностей связана с методом наименьших квадратов (рисунок 2, страница 136), цель которого — представление полученных данных в виде кривой, а также минимизация погрешностей метода. Лежандр представил этот метод в 1805 году в труде «Новые методы для определения орбит комет». Кроме этого молодой математик по имени Карл Фридрих Гаусс утверждал, будто он первым использовал этот метод в 1801 году, что спровоцировало ожесточенный спор между двумя математиками, каждый из которых отстаивал свое право на авторство открытия.

Гаусс первым рассчитал орбиту планеты Церера, открытой в начале XIX века, 1 января 1801 года. Немецкий ученый проанализировал серию наблюдений Цереры, предположил, как проходит ее орбита, и предсказал, где эта малая планета появится снова. Ученый использовал собственный метод — метод наименьших квадратов, который тщательно описал в своем дневнике. Он позволяет построить траекторию на основании совокупности точек и минимизировать при этом сумму квадратов погрешностей, то есть различие между наблюдаемыми и реальными значениями.

В 1809 году Гаусс триумфально вошел в мир астрономии со своим трудом «Теория движения небесных тел». В нем он устанавливал связь между методом наименьших квадратов и теорией погрешностей, доказывая, что распределение погрешностей может быть проанализировано с помощью этого метода. В действительности однажды, определяя кривую, которая позволяла минимизировать среднюю квадратичную погрешность, Гаусс заметил, что погрешности приближенного значения распределяются случайным образом вокруг среднего значения. Это симметричное распределение в виде купола было не чем иным, как кривой Гаусса (рисунок 3, ниже). Она может быть выражена в виде функции: