Joaquin Sandalinas - До предела чисел. Эйлер. Математический анализ.

389965026819938 = 5569 + 389965026814369.

Гольдбах родился в Пруссии, но большую часть своей жизни провел в России, где искал новые таланты для Петербургской академии и работал в ней же секретарем. Он дружил с Лейбницем, Абрахамом де Муавром, Николаем Бернулли (а также с другими членами этой выдающейся семьи) и Эйлером, чью кандидатуру он усиленно продвигал и в переезде которого в Россию сыграл решающую роль. Он даже стал учителем царевича Петра II и занимал высокие посты в министерстве иностранных дел, где работал криптографом. Гольдбах занимался разными областями науки и добился хороших результатов в изучении числовых последовательностей, в особенности благодаря сотрудничеству с Эйлером. Личность последнего, видимо, стимулировала Гольдбаха в работе. Например, не все знают, что именно Гольдбах, будучи не в состоянии решить Базельскую задачу самостоятельно, привлек к ней Эйлера, который впоследствии прославился найденным решением. Переписка Эйлера и Гольдбаха, необыкновенно обширная и полная математических рассуждений, насчитывает почти 200 писем. Об уважении, которое Эйлер питал к Гольдбаху, свидетельствует хотя бы тот факт, что он выбрал коллегу крестным отцом своего первенца.

Сегодня о Гольдбахе вспоминают не в связи с его теоремами, а с проблемой, носящей его имя. В 1992 году вышел роман "Дядя Петрос и проблема Гольдбаха" Апостолоса Доксиадиса. Издательство Faber&Faber предложило премию в миллион долларов, действительную два года, тому, кто найдет решение. Скорее всего, издатели знали, что никакого ответа они не получат. Пока эта проблема решена только в испанском художественном фильме 2007 года "Западня Ферма" режиссеров Луиса Пьедраиты и Родриго Сопеньи.

В этой паре, не так давно найденной нумерологом Йоргом Рихстейном, одно слагаемое состоит из четырех цифр, а второе — из 15, при этом оба они являются простыми числами. До сих пор никому не удалось доказать ни одну из двух гипотез. Слабую можно считать почти доказанной, поскольку известно, что она работает для всех чисел больше 10 346. Чтобы доказать ее полностью, надо разобраться с нерешенными случаями: начать с 7 и дойти до 10 1346. Это очень сложно: любой существующей вычислительной машине потребуется на это большее количество секунд, чем число атомов во Вселенной.

С сильной проблемой Гольдбаха ситуация яснее: ни одного ее доказательства не существует. Найти его не удалось даже Эйлеру. С помощью супервычислителей Cray проблему проверили для огромных чисел, доходящих до 10 18, но общее доказательство так и не найдено. Тем не менее математикам удалось добиться значительных результатов. Например, китайский ученый Чен Джингрун (1933-1996) в 1966 году доказал, что каждое достаточно большое число можно представить в виде суммы двух других, из которых одно — простое, а второе — произведение максимум двух простых.

Вариационное исчисление может считаться обобщенным исчислением и поэтому однозначно является частью анализа. Его цель заключается в нахождении пути, кривой, поверхности и так далее, для которых определенная функция имеет стационарное значение — как правило, максимальное или минимальное. Исчисление имеет основополагающее значение для физики, в частности в таких областях практического применения, как теория упругости и баллистика, которые вызывали большой интерес уже во времена Эйлера. Неудивительно, что ученый пришел к вариационному исчислению в 1744 году, через три года после переезда в Берлин, когда он занялся физикой, а именно принципом наименьшего действия в механике.

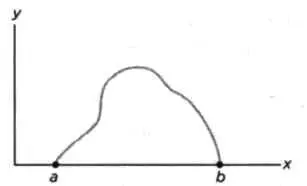
РИС. 5

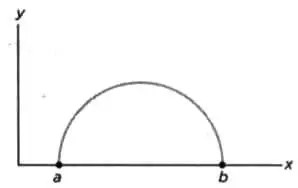
РИС . б

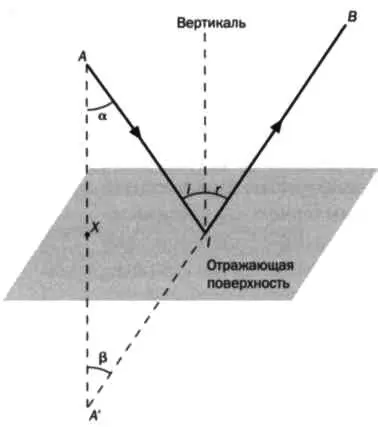
РИС. 7

Путь, пройденный лучом света на поверхности от А до В, равен отрезку А’ В. Следовательно, он проходит наименьшее расстояние.

Как и все основные проблемы в математике, вопрос о максимумах и минимумах имел длинную историю. Достаточно вспомнить классическую задачу — или, скорее, легенду — о Ди- доне, королеве Тира. Она бежала с последними оставшимися ей верными людьми и достигла берегов, на которых ей суждено было создать свое царство, Карфаген. Она попросила местного короля Иарбанта дать ей кусок земли, где могли бы жить ее подданные. Тот согласился с одним условием: владения Дидоны должны быть равны площади, которую она сможет покрыть воловьей шкурой. Чтобы упростить объяснение, представим, что побережье — прямая линия, без заливов, бухт и мысов. Царица разрезала шкуру на тончайшие ремешки так, что получилась длинная веревка. Она соединила ее концы (рисунок 5), а затем применила базовый принцип изопериметров, то есть площадей, периметры которых имеют одинаковую длину. Одна часть этого периметра проходила вдоль моря, а оставшаяся должна была охватить как можно большую площадь. Решение состояло в том, что веревка из воловьей кожи должна располагаться в виде полукруга, диаметр которого — побережье (рисунок 6). Задача Дидоны относится к разряду классических изопериметриче- ских задач, которые часто встречаются в физике. Она относится к более широкой категории задач, похожих друг на друга, поскольку в них всегда надо найти экстремум функционала — максимум или минимум — при заданных неизменных условиях. Существует наглядный и к тому же очень древний пример, автором которого является Герон Александрийский (ок. 10- 70). Он задался вопросом об отражении света, заметив, что луч, идущий от А к В, отражаясь от зеркала, следует по самой короткой траектории (рисунок 7).

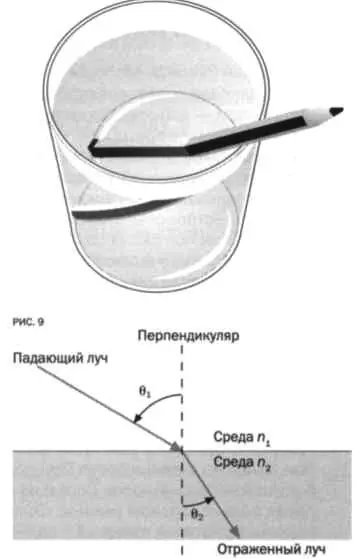
РИС. 8

РИС. 10

Впоследствии Ферма сформулировал закон о преломлении света (так называемый закон Снеллиуса), по которому n 1, sinθ 1= n 2sinθ 2Однако в этом случае пройденное расстояние не было минимальным. Минимальным было время, за которое луч проходит от A до B, а расстояние на самом деле было, как мы сказали бы сегодня, функцией времени: e = v · t, где v — скорость луча света в преломляющей его среде. Таким образом, минимизируется функция ƒ(t) · vt (рисунки 8-9).