Joaquin Sandalinas - До предела чисел. Эйлер. Математический анализ.

треугольника), располагаются на одной прямой, впоследствии названной прямой Эйлера. Если треугольник равнобедренный, то на этой линии находится еще и инцентр (точка пересечения трех биссектрис). О центре окружности Эйлера ( мы поговорим ниже.

Помимо того что обнаружилось расположение на одной прямой точек О, В и С, удалось получить точное соотношение:

2d(B,C) = d(B,0).

Как видите, расстояние между барицентром и ортоцентром всегда в два раза больше расстояния между барицентром и центром описанной окружности (рисунок 11). И хотя, как мы уже сказали, инцентр располагается на той же прямой только в равнобедренном треугольнике, Эйлер нашел формулу, по которой можно рассчитать расстояние между инцентром и центром описанной окружности:

d 2= R(R-2r),

где R и r — радиусы описанной и вписанной окружностей соответственно.

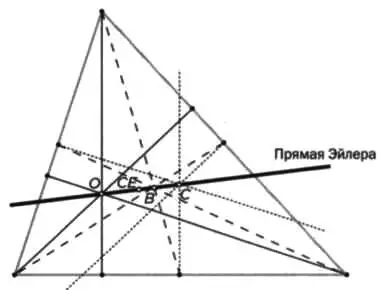
РИС. 11

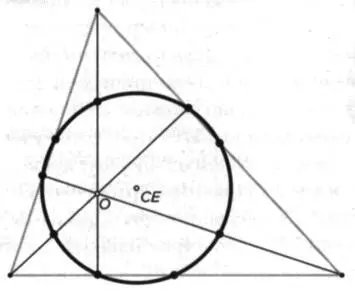
РИС. 12

Крыша олимпийского стадиона в Монако занимает наименьшую площадь, рассчитанную с помощью вариационного исчислении.

В 1750 году Эйлер обнародовал мегаскоп — прибор дли проецировании непрозрачных тел. Он состоил из двух вогнутых зеркал и двух ламп.

Марка, изображающей теорему для многогранников — одно из высочайших достижений Эйлера.

Центром треугольника называется точка Р, которая обладает особым геометрическим свойством по отношению к определенным линиям (высотам, медианам, биссектрисам и так далее) и определяет окружности или другие простые фигуры, обладающие некоторыми свойствами, связанными с исходным треугольником. Это очень туманное определение, но к нему можно добавить условие: точка Р должна быть инвариантом по отношению к симметриям, вращениям и расширениям. Примерами таких центров являются ставшие уже классическими ортоцентр, центр описанной окружности и инцентр, но существуют и другие. Статья Эйлера о центрах треугольника вызывала удивление у геометров (они полагали, что об особых точках этой фигуры уже сказано все), однако в последующие годы было открыто много других центров. Сегодня существуют сайты, посвященные их перечислению и изучению: например, Encyclopedia of Triangle Centers Кларка Кимберлин- га насчитывает более 3500 точек.

Через несколько лет после этого Карл Вильгельм Фейербах (1800-1834) и Олри Теркем (1782-1862) нашли окружность с центром СE, известную сегодня как окружность Эйлера. Она проходит через девять точек: через середины всех сторон треугольника, через основания всех его высот и, наконец, через срединную точку отрезка, идущего от каждой вершины к ортоцентру (рисунок 12). Существует еще одно соотношение, касающееся этих расстояний:

d (СЕ,O) = d (СЕ,С).

Некоторые из его простейших открытий таковы, что можно представить себе дух Евклида, вопрошающий: "Почему при жизни на Земле я не додумался до этого?"

Гарольд Коксетер об Эйлере

Как легко догадаться, центры треугольников были не единственным геометрическим интересом Эйлера. Мы могли бы перечислить множество других занимавших его вопросов, но среди них есть один, который отличается своей сложностью, прямо пропорциональной простоте формулировки. В 1751 году Эйлер в письме Гольдбаху предложил следующую задачу: найти для любого выпуклого многоугольника с п сторонами, сколькими способами можно разделить его на треугольника при помощи диагоналей, которые не должны пересекаться, и считая по отдельности разные углы. Эйлер спрашивал, сколько поперечных разрезов надо сделать в "торте" многоугольника, как видно на рисунке. Это сложная задача на комбинаторику, и ее решение — С n-2, где

C n= 1/n( 2n n-1)

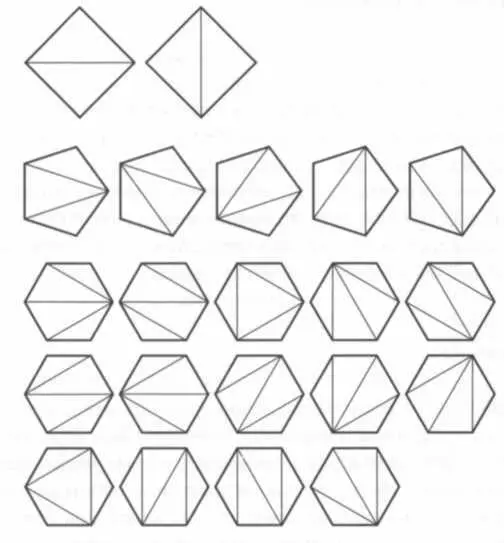
Все возможные способы разделения на треугольники многоугольников с 4,5 и 6 сторонами при помощи нелересекающихся диагоналей.

Эйлер интересовался всем и писал статьи почти по всем вопросам. Многие из них сложно отнести к той или иной области науки, известной в то время: к чему относится, например, задача о возможном маршруте по мостам Кенигсберга? Другие же, напротив, прекрасно вписывались в мир того времени, например задача о выплате пенсий, но не были первоочередными проблемами. Краткий экскурс по этим трудноклассифицируемым сочинениям даст более глубокое представление о необыкновенном разнообразии наследия Эйлера.

Вклад Эйлера в практическое инженерное дело обычно принижается, отчасти из-за невысокого мнения о нем Фридриха II, который считал очевидным, что все проекты, реализованные его подданными, будь то генералы, садовники или ученые, должны прекрасно работать, ведь за это он им и платил. Инженеры Его Величества — а Эйлер был их начальником — не были исключением. Если, например, из фонтанов в садах императора вдруг не била струя, то, по мнению Фридриха, это означало, что его инженеры и конструкторы никуда не годятся. Ошибки в расчетах давления воды не прощались.

Несмотря на такое отношение, Эйлер много занимался задачами практической инженерии. Около 1744 года (правда, эта работа была опубликована только в 1757-м) он применил вариационное исчисление к рассчету нагрузки от предметов на пилястрах, которые их поддерживают, — на профессиональном языке это называется критической нагрузкой, простым вариантом деформации.

Представим себе колонну, как на следующей странице, на которую давит осевая концентрическая сила, q, то есть груз, давящий на центр тяжести ее поперечной секции. Эйлер нашел формулу

F = π 2EI/(KL) 2,

которая описывает эту нестабильность, где F — сила, или осевой груз, Е — модуль упругости, I — момент инерции площади, L — длина между точками опоры колонны, а — эмпирический фактор, зависящий от условий поддержки конца перекладины или колонны, испытывающей деформацию. Произведение KL определяет их действительную длину.

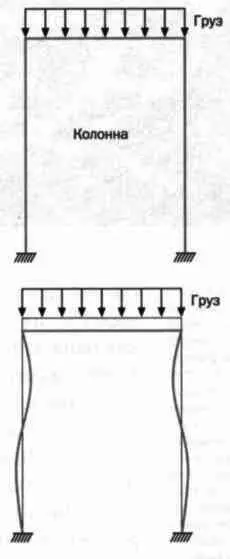
Деформация или нестабильность при критической нагрузке колонны.