Ричард Фейнман - 9. Квантовая механика II

В итоге

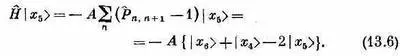
Когда гамильтониан действует на состояние | x 5>, то возни­кает некоторая амплитуда оказаться в состояниях | x 4> и | х 6> . Это просто означает, что существует определенная амплитуда того, что направленный книзу спин перепрыгнет к соседнему атому. Значит, из-за взаимодействия между спинами, если вна­чале один спин был направлен вниз, имеется некоторая ве­роятность того, что позднее вместо него вниз будет смотреть другой. При действии на состояние | х n >гамильтониан дает

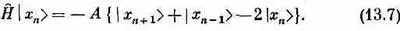
Заметьте, в частности, что если взять полную систему состоя­ний только с одним спином-«перевертышем», то они будут перемешиваться только между собой. Гамильтониан никогда не перемешает эти состояния с другими, в которых спинов-«перевертышей» больше. Пока вы только обмениваетесь спинами, вы никогда не сможете изменить общего количества перевертышей. Удобно будет использовать для гамильтониана матричное обозначение, скажем,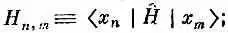

уравнение (13.7) эквивалентно следующему:

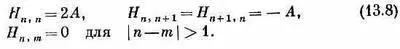
Каковы же теперь уровни энергии для состояний с одним перевернутым спином? Пусть, как обычно, С n — амплитуда того, что некоторое состояние |y> находится в состоянии | x n >. Если мы хотим, чтобы |y> было состоянием с определенной энергией, то все С n обязаны одинаково меняться со временем, а именно по правилу

Подставим это пробное решение в наше обычное уравнение Гамильтона

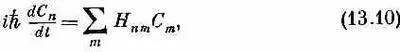
используя в качестве матричных элементов (13.8). Мы, конечно, получим бесконечное количество уравнений, но все их можно будет записать в виде

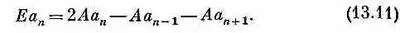
Перед нами опять в точности та же задача, что и в гл. 11, только там, где раньше стояло Е 0 , теперь стоит 2 А. Решения отвечают амплитудам С n (амплитудам с перевернутым спином), которые распространяются вдоль решетки с константой распростране­ния k и энергией

Е =2 A (1-coskb) , (13.12)

где b — постоянная решетки.

Решения с определенной энергией отвечают «волнам» перево­рота спина, называемым «спиновыми волнами». И для каждой длины волны имеется соответствующая энергия. Для больших длин волн (малых k ) эта энергия меняется по закону

Е=Аb 2 k 2 . (13.13)

Как и прежде, мы можем теперь взять локализованный волно­вой пакет (содержащий, однако, только длинные волны), кото­рый соответствует тому, что электрон-«перевертыш» окажется в такой-то части решетки. Этот перевернутый спин будет вести себя как «частица». Так как ее энергия связана с k формулой (13.13), то эффективная масса «частицы» будет равна

Такие «частицы» иногда именуют «магнонами».

§ 2. Две спиновые волны

Теперь мы хотели бы выяснить, что происходит, когда име­ется пара перевернутых спинов. Опять начнем с выбора системы базисных состояний. Выберем такие состояния, когда спины перевернуты в каких-то двух местах (так, как на фиг. 13.2).

Фиг. 13.2. Состояния с двумя переверну­тыми спинами.

Эти состояния можно, скажем, отмечать x -координатами тех двух узлов решетки, в которых оказались электроны с пе­ревернутым спином. То, что на рисунке, можно обозначить | х 2 , х 5> . В общем случае базисные состояния будут | х n , х m >— дважды бесконечная совокупность! При таком способе описания состояние | x 4 , х 9 > и состояние | х 9 , x 4> совпадают, потому что каждое из них просто говорит, что в точках 4 и 9 спин перевер­нут; порядок их не имеет значения. Не имеет также смысла состояние | x 4, х 4> — такого просто быть не может. Любое со­стояние |y> мы можем описать, задав амплитуды того, что оно обнаружится в одном из базисных состояний.

Итак, С m , n =<���х m ,х n |y> теперь означает амплитуду того, что система в состоянии |y> окажется в состоянии, когда у электронов, стоящих вблизи m -го и n -го атомов, спины смотрят вниз. Сложности, которые теперь возникнут, будут связаны не с усложнением идей,— это будут просто усложнения в бухгалтерии. (Одна из сложностей квантовой механики как раз и состоит в громоздкости бухгалтерии. Чем больше спинов перевернется, тем сложнее станут обозначения, тем больше будет индексов, тем страшнее будут выглядеть уравнения; но сами идеи вовсе не обязательно должны усложниться.)

Уравнения движения спиновой системы — это дифферен­циальные уравнения для С n , m :

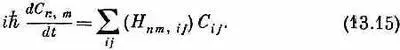
Пусть нам опять нужно найти стационарные состояния. Как обычно, производные по времени обратятся в Е, умноженное на амплитуду, a C m , n , заменятся коэффициентами а m , n . Затем надо аккуратно рассчитать влияние Н на состояние с перевернутыми спинами т и п. Это сделать нетрудно. Представьте на минуту, что т далеко от n, так что не нужно думать, что будет, если ... и т. д. Обменная операция, производимая в точке х n , передвинет перевернутый спин либо к (n +1)-му, либо к ( n -1)-му атому, так что имеется ненулевая амплитуда того, что теперешнее состояние получилось из состояния |х m , х n +1> , и амплитуда того, что оно произошло из состояния |х m , х n - 1> . Но передви­нуться мог и второй спин, так что не исключена и какая-то амплитуда того, что С m , n питается от С m +1 , n или от С m - 1 , n . Все эти эффекты должны быть одинаковы. Окончательный вид гамильтонова уравнения для С m.n таков: