Ричард Фейнман - 9. Квантовая механика II

Достигая барьера, эти носители по-прежнему будут видеть перед собой идущий под гору потенциал и будут все скатываться в p -область. (Если D V больше естественной разности потенциа­лов V, положение может измениться, но что случается при таких высоких напряжениях, мы рассматривать не будем.) В итоге ток положительных носителей I , текущий через переход, будет определяться разницей токов в обе стороны:

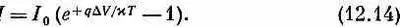
Дырочный ток I течет в n -область. Там дырки диффундируют в самую глубь n -области и могут, вообще говоря, аннигилиро­вать на основной массе отрицательных носителей электронов. Убыль электронов, теряемых при этой аннигиляции, воспол­няется током электронов из внешнего контакта материала n -типа.

Когда D V =0, то и ток в (12.14) равен нулю. Если D V положительна, ток с напряжением резко растет, а если D V отрицательна, знак тока меняется, но экспоненциальный член вскоре становится пренебрежимо малым, и отрицательный ток никогда не превышает I 0— величины, которая, по нашему предположению, очень мала. Этот обратный ток I 0ограничен той слабой плотностью, которой обладают неосновные носители в n -области перехода.

Если вы проведете в точности тот же анализ для тока отри­цательных носителей, текущего через переход, сперва без внешней разности потенциалов, а после с небольшой приложен­ной извне разностью потенциалов D V , то для суммарного электронного тока вы опять получите уравнение, похожее на (12.14). Поскольку полный ток есть сумма токов носите­лей обоего рода, то (12.14) применимо и к полному току, если только отождествить I 0с максимальным током, кото­рый может течь при переме­не знака напряжения.

Вольтамперная характеристика (12.14) показана на фиг. 12.10.

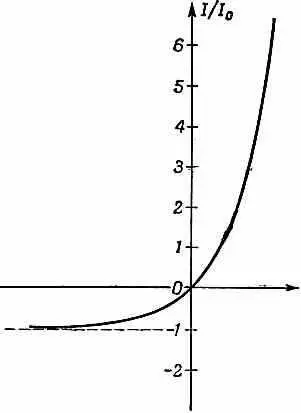
Фиг. 12.10. Зависимость тока через переход от приложенного к нему напряжения.

Она демонстрирует нам типичное поведение кристаллических диодов, подобных тем, которые применяются в современных вычислительных машинах. Нужно только заметить, что (12.14) справедливо лишь при невысоких напряжениях. При напряже­ниях, сравнимых с естественной внутренней разностью потен­циалов V (или превышающих ее), в игру входят новые явления и ток уже не подчиняется столь простому уравнению.

Быть может, вы вспомните, что в точности такое же уравне­ние мы получили, говоря о «механическом выпрямителе» — храповике и собачке [см. гл. 46 (вып. 4)]. Мы получали те же уравнения, потому что лежащие в их основе физические про­цессы весьма схожи.

§ 6. Транзистор

Пожалуй, самым важным применением полупроводников является изобретение транзистора. Состоит он из двух полу­проводниковых переходов, расположенных вплотную друг к другу, и работа его частично опирается на те же принципы, которые мы только что описывали, говоря о полупроводниковом диоде — выпрямляющем переходе. Предположим, что мы изго­товили из германия небольшой брусочек, составленный из трех участков: p -область, n- область и опять p -область (фиг. 12.11,а). Такое сочетание именуется p—n—p -транзистором. Ведут себя эти переходы в транзисторе примерно так же, как описывалось в предыдущем параграфе. В частности, в каждом переходе должен наблюдаться перепад потенциала — падение потенци­ала из n -области в каждую из p -областей. Если внутренние свой­ства обеих p -областей одинаковы, то потенциал вдоль брусочка меняется так, как показано на фиг. 12.11, б .

Теперь представьте себе, что каждая из трех областей под­ключена к источнику внешнего напряжения (фиг. 12.12, а ). Будем относить все напряжения к контакту, присоединенному к левой p -области, так что на этом контакте потенциал будет равен нулю.

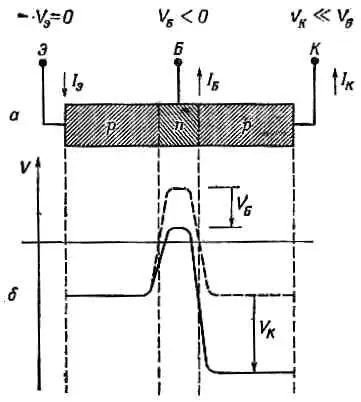
Фиг. 12.12. Распределение потенциала в работающем транзисторе.

Этот контакт мы назовем эмиттером; n -область называется базой, или основанием, к ней подведен слабый отри­цательный потенциал; правая p -область называется коллекто­ром, к ней подведен намного больший отрицательный потенциал. В таких условиях потенциал будет меняться вдоль кристалла так, как показано на фиг. 12.12,б.

Посмотрим сначала, что происходит с положительными носителями, потому что именно их поведение в первую очередь управляет работой p—n—p -транзистора. Раз потенциал эмит­тера более положителен, нежели потенциал базы, то из эмит­тера в базу пойдет ток положительных носителей. Ток этот до­вольно велик, потому что перед нами переход, работающий при «подталкивающем напряжении» (что отвечает правой половине кривой на фиг. 12.10). При таких условиях положительные но­сители, или дырки, будут «эмиттироваться» из p -области в n -область. Может показаться, что этот ток вытечет из n -области через контакт Б. Но здесь-то и таится секрет транзи­стора. Эта n -область делается очень узкой, толщиной обычно в 10 -3 см , а то и уже, намного уже, чем ее поперечные размеры. Следовательно, у дырок, попавших в га-область, имеется очень большой шанс успеть продиффундировать через всю область до следующего перехода, прежде чем они аннигилируют с элект­ронами re-области. А когда они подойдут к правой границе n -области, они обнаружат перед собой крутой спуск с потен­циального холма и сходу ссыплются в правую p -область. Эта сторона кристалла называется коллектором, потому что он собирает дырки после того, как они проскользнут через n -область. В типичном транзисторе почти весь дырочный ток, вы­шедший из эмиттера и попавший на базу, собирается в области коллектора, и только жалкие остатки (доли процента) вклю­чаются в суммарный ток с электрода базы. Сумма токов из базы и коллектора, естественно, равна току через эмиттер.

Теперь представим себе, что получится, если мы будем слегка менять потенциал V бконтакта. Поскольку мы находимся на сравнительно крутой части кривой фиг. 12.10, легкие изменения потенциала V бдовольно значительно отразятся на токе эмиттера I Э. А напряжение на коллекторе V Kнамного более отрицательно, чем напряжение на электроде базы, и эти слабые изменения потенциала не скажутся заметно на крутом потенциальном холме между базой и коллектором. Большинство положительных носителей, испущенных в n -область, по-прежнему будут попадать в коллектор. Итак, изме­нениям потенциала электрода базы будут отвечать изме­нения тока через коллектор I K. Существенно, однако, что ток через базу I Бвсе время будет составлять лишь небольшую часть тока через коллектор. Транзистор — это усилитель; не­большой ток I б, проходящий через электрод базы, приведет к сильному току (раз в 100 сильней, а то и больше) через коллек­торный электрод.