Ричард Фейнман - 9. Квантовая механика II

Разность потенциалов между верхом и низом кристалла равна, естественно, этой самой напряженности электрического поля, умноженной на высоту кристалла. Напряженность электриче­ского поля в кристалле x ┴пропорциональна плотности тока и напряженности магнитного поля. Множитель пропорциональ­ности 1/qN называется коэффициентом Холла и обычно изобра­жается символом R H . Коэффициент Холла зависит просто от плотности носителей при условии, что носители одного знака находятся в явном большинстве. Поэтому измерение эффекта Холла дает удобный способ опытным путем определять плот­ность носителей в полупроводнике.

§ 4. Переходы между полупроводниками

Теперь мы хотим выяснить, что получится, если взять два куска германия или кремния с неодинаковыми внутренними характеристиками, скажем с разным количеством примеси, и приложить их друг к другу, чтобы возник «переход». Начнем с того, что именуется p—n -переходом, когда с одной стороны границы стоит германий p -типа, а с другой — германий n -типа (фиг. 12.8).

Фиг. 12.8. p — n-переход.

Практически не очень удобно прикладывать друг к другу два разных куска германия и добиваться однородности контакта между ними на атомном уровне. Вместо этого переходы делают из одного кристалла, обработанного в разных концах по-разному. Один из приемов состоит в том, чтобы после того, как из расплава была выращена половинка кристалла, добавить в оставшийся расплав подходящую присадку. Другой способ — это нанести на поверхность немного примесного элемента и затем подогреть кристалл, чтобы часть атомов примеси продиффундировала в тело кристалла. У сделанных такими способами переходов нет резкой границы, хотя сами границы могут быть сделаны очень тонкими — до 10 -4 см. Для наших рассуждений мы вообразим идеальный случай, когда эти две области кристалла с разными свойствами резко разграничены. В n -области p—n -перехода имеются свободные электроны, которые могут переходить с места на место, а также фиксиро­ванные донорные узлы, которые уравновешивают полный электрический заряд. В p -области имеются свободные дырки, тоже переходящие с места на место, и равное количество отри­цательных акцепторных узлов, гасящих полный заряд. Но в дей­ствительности такое описание положения вещей годится лишь до тех пор, пока между материалами не осуществлен контакт. Как только материалы соединятся, положение на границе из­менится. Теперь, достигнув границы в материале n -типа, элект­роны не отразятся обратно, как это было бы на свободной по­верхности, а смогут прямо перейти в материал p -типа. Часть электронов из материала n -типа поэтому будет стремиться про­скользнуть в материал p -типа, где электронов меньше. Но так длиться без конца не может, потому что по мере того, как в n -области будут теряться электроны, ее заряд начнет стано­виться все более положительным, пока не возникнет электри­ческое напряжение, которое затормозит диффузию электронов в p -область. Подобным же образом положительные но­сители из материала p -типа смогут проскальзывать через переход в материал n -типа, оставляя позади себя избы­ток отрицательного заряда. В условиях равновесия пол­ный ток диффузии должен будет равняться нулю. Это произойдет благодаря возни­кновению электрических полей, которые установятся таким образом, чтобы возвращать положительные носители обратно в p -область.

Оба описанных нами процесса диффузии продолжаются одно­временно, и оба, как видите, действуют в таком направлении, чтобы материал n -типа зарядить положительно, а материал p -типа — отрицательно. Вследствие конечной проводимости полупроводящих материалов изменение потенциала между p -областью и n -областью произойдет в сравнительно узком участке близ границы; в основной же массе каждой области потенциал будет однороден. Проведем перпендикулярно гра­нице ось х. Тогда электрический потенциал будет меняться с х так, как показано на фиг. 12.9, б .

Фиг. 12,9. Электрический по­тенциал и плотности носителей в полупроводниковом переходе без смещающего напряжения.

На фиг. 12.9, в показано ожи­даемое изменение плотности N n n -носителей и плотности N p p -носителей. Вдали от перехода плотности носителей N p и N n должны быть попросту равны той равновесной плотности, кото­рой положено устанавливаться в определенном бруске того же материала при той же температуре. (Фиг. 12.9 вычерчена для перехода, в котором в материале p -типа примеси больше, чем в материале n -типа.) Из-за перепада потенциала на переходе положительным носителям приходится взбираться на потен­циальный холм, чтобы попасть в p -область. Это означает, что в условиях равновесия в материале re-типа будет меньше поло­жительных носителей, чем в материале p -типа. Можно ожидать (вспомните законы статистической механики), что отношение количеств носителей p -типа в обеих областях будет даваться уравнением

Произведение q p V в числителе показателя экспоненты — это как раз та энергия, которая требуется, чтобы пронести заряд q p сквозь разность потенциалов V.

Точно такое же уравнение существует и для плотностей но­сителей n -типа:

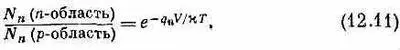
Если мы знаем равновесные плотности в каждом из двух мате­риалов, то любое из этих уравнений даст нам разность потен­циалов на переходе.

Заметьте, что для того, чтобы (12.10) и (12.11) давали оди­наковые значения разности потенциалов V , произведение N p N n должно быть в p -области и в n -области одним и тем же.

Фаг. 12.11. Распределение по­тенциала вдоль транзистора, если не приложено напряжение.

(Вспомните, что q n =- q p .) Но мы еще раньше видели, что это произведение зависит только от температуры и от ширины энергетической щели кристалла. Если обе части кристалла находятся при одинаковой температуре, оба уравнения будут совместны, давая одинаковое значение разности потенциалов.