Ричард Фейнман - 9. Квантовая механика II

I могли добираться до электродов, не боясь захвата. Потому и используются кремний и германий, что образцы этих полупро­водников разумных размеров (порядка сантиметра) можно по­лучать большой чистоты.

До сих пор мы касались только свойств полупроводниковых кристаллов при температурах около абсолютного нуля. При любой ненулевой температуре имеется еще другой механизм создания пар электрон — дырка. Энергией пару может снаб­дить тепловая энергия кристалла. Тепловые колебания кристал­ла могут передавать паре свою энергию, вызывая «самопроиз­вольное» рождение пар.

Вероятность (в единицу времени) того, что энергия, дости­гающая величины энергетической щели E щели, сосредоточится в месте расположения одного из атомов, пропорциональна ехр(- Е щеяи /kТ), где Т— температура, а k — постоянная Больц­мана [см. гл. 40 (вып. 4)]. Вблизи абсолютного нуля вероятность эта мало заметна, но по мере роста температуры вероятность образования таких пар возрастает. Образование пар при любой конечной температуре должно продолжаться без конца, давая все время с постоянной скоростью все новые и новые положи­тельные и отрицательные носители. Конечно, на самом деле этого не будет, потому что через мгновение электроны случайно снова повстречаются с дырками, электрон скатится в дырку, а освобожденная энергия перейдет к решетке. Мы скажем, что электрон с дыркой «аннигилировали». Имеется определенная вероятность того, что дырка встретится с электроном и оба они друг друга уничтожат.

Если количество электронов в единице объема есть N n (n означает негативных, или отрицательных, носителей), а плот­ность положительных (позитивных) носителей N p , то вероят­ность того, что за единицу времени электрон с дыркой встре­тятся и проаннигилируют, пропорциональна произведению N n N p . При равновесии эта скорость должна равняться ско­рости, с какой образуются пары. Стало быть, при равновесии произведение N n N p должно равняться произведению некото­рой постоянной на больцмановский множитель

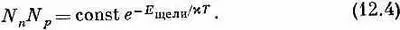
Говоря о постоянной, мы имеем в виду ее примерное постоянство. Более полная теория, учитывающая различные детали того, как электроны с дырками «находят» друг друга, свидетельствует, что «постоянная» слегка зависит и от температуры; но главная зависимость от температуры лежит все же в экспоненте.

Возьмем, например, чистое вещество, первоначально бывшее нейтральным. При конечной температуре можно ожидать, что число положительных и отрицательных носителей будет одно и то же, N n = N р . Значит, каждое из этих чисел должно с температурой меняться как 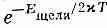. Изменение мно­гих свойств полупроводника (например, его проводимости) определяется главным образом экспоненциальным множителем, потому что все другие факторы намного слабее зависят от тем­пературы. Ширина щели для германия примерно равна 0,72 эв, а для кремния 1,1 эв.

При комнатной температуре k Т составляет около 1/ 40 эв. При таких температурах уже есть достаточно дырок и электро­нов чтобы обеспечить заметную проводимость, тогда как, ска­жем, при 30°К (одной десятой комнатной температуры) прово­димость незаметна. Ширина щели у алмаза равна 6—7 эв, по­этому при комнатной температуре алмаз — хороший изолятор.

§ 2. Примесные полупроводники

До сих пор мы говорили только о двух путях введения доба­вочных электронов в кристаллическую решетку, которая во всем остальном совершенно идеальна. Один путь — это впрыс­нуть электрон от внешнего источника, а другой — выбить связанный электрон из нейтрального атома, сотворив одновре­менно и электрон и дырку. Но можно внедрить электроны в зону проводимости кристалла совершенно иным способом. Представим себе кристалл германия, в котором один из атомов германия заменен атомом мышьяка. У атомов германия валент­ность равна 4, и кристаллическая структура контролируется четырьмя валентными электронами. А у мышьяка валентность равна 5. И вот оказывается, что отдельный атом мышьяка в состоянии засесть в решетке германия (потому что габариты у него как раз такие, как надо), но при этом он будет вынужден действовать как четырехвалентный атом, тратя четыре валент­ных электрона из своего запаса на создание кристаллических связей и отбрасывая пятый. Этот лишний электрон привязан к нему очень слабо — энергия связи менее 1/ 10 эв. При комнат­ной температуре электрон с легкостью раздобудет такую не­большую энергию у тепловой энергии кристалла и отправится на свой страх и риск блуждать по решетке на правах свобод­ного электрона. Примесный атом наподобие мышьяка назы­вается донорным узлом, потому что он может снабдить кристалл отрицательным носителем. Если кристалл германия выращи­вается из расплава, куда было добавлено небольшое количество мышьяка, то мышьяковые донорские пункты распределятся по всему кристаллу и у кристалла появится определенная плот­ность внедренных отрицательных носителей.

Могло бы показаться, что малейшее электрическое поле, приложенное к кристаллу, смело бы эти носители прочь. Но этого не случится, ведь каждый атом мышьяка в теле кристалла заряжен положительно. Чтобы весь кристалл оставался нейт­ральным, средняя плотность отрицательных носителей — элект­ронов — должна быть равна плотности донорных узлов. Если вы приложите к граням этого кристалла два электрода и подключите их к батарейке, пойдет ток; но если с одного конца уносятся электроны-носители, то на другой конец должны по­ступать свежие электроны проводимости, так что средняя плотность электронов проводимости остается все время пример­но равной плотности донорных узлов.

Поскольку донорные узлы заряжены положительно, у них должно наблюдаться стремление перехватывать некоторые из электронов проводимости, когда последние блуждают по кри­сталлу. Поэтому донорный узел должен действовать как раз как та ловушка, о которой мы говорили в предыдущем пара­графе. Но если энергия захвата достаточно мала (как у мышья­ка, например), то общее число захваченных в какой-то момент носителей должно составлять лишь малую часть их общего числа. Для полного понимания поведения полупроводников этот захват, конечно, следует иметь в виду. Однако мы в даль­нейшем будем считать, что энергия захвата настолько низка, а температура так высока, что на донорных узлах нет элект­ронов. Конечно, это всего-навсего приближение.