Ричард Фейнман - 9. Квантовая механика II

Для энергий возле дна зоны формулу (12.1) можно прибли­зительно записать так:

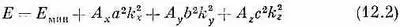
(см. гл. 11, § 4).

Если нас интересует движение электрона в некотором опре­деленном направлении, так что отношение компонент kвсе время одно и то же, то энергия есть квадратичная функция волнового числа и, значит, импульса электрона. Можно напи­сать

где a — некоторая постоянная, и начертить график зависимости Е от k (фиг. 12.1).

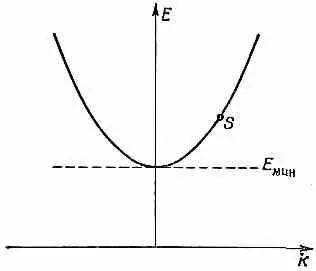
Фиг. 12.1. Энергетическая диаг­рамма для электрона в кристалле изолятора.

Такой график мы будем называть «энергетиче­ской диаграммой». Электрон в определенном состоянии энергии и импульса можно на таком графике изобразить точкой ( S на рисунке).

Мы уже упоминали в гл. 11, что такое же положение вещей возникнет, если мы уберем электрон из нейтрального изолятора. Тогда на это место сможет перепрыгнуть электрон от соседнего атома. Он заполнит «дырку», а сам оставит на том месте, где стоял, новую «дырку». Такое поведение мы можем описать, задав амплитуду того, что дырка окажется возле данного опре­деленного атома, и говоря, что дырка может прыгать от атома к атому. (Причем ясно, что амплитуда А того, что дырка пере­прыгивает от атома а к атому b , в точности равна амплитуде того, что электрон от атома b прыгает в дырку от атома а.)

Математика для дырки такая же, как для добавочного элект­рона, и мы опять обнаруживаем, что энергия дырки связана с ее волновым числом уравнением, в точности совпадающим с (12.1) и (12.2), но, конечно, с другими численными значениями амплитуд А х , A y и А z . У дырки тоже есть энергия, связанная с волновым числом ее амплитуд вероятности. Энергия ее лежит в некоторой ограниченной зоне и близ дна зоны квадратично меняется с ростом волнового числа (или импульса) так же, как на фиг. 12.1. Повторяя наши рассуждения гл. 11, § 3, мы обна­ружим, что дырка тоже ведет себя как классическая частица с какой-то определенной эффективной массой, с той только раз­ницей, что в некубических кристаллах масса зависит от направ­ления движения. Итак, дырка напоминает частицу с положи­тельным зарядом, движущуюся сквозь кристалл. Заряд ча­стицы-дырки положителен, потому что она сосредоточена в том месте, где нет электрона; и когда она движется в какую-то сто­рону, то на самом деле это в обратную сторону движутся электроны.

Если в нейтральный кристалл поместить несколько электро­нов, то их движение будет очень похоже на движение атомов в газе, находящемся под низким давлением. Если их не слишком много, их взаимодействием можно будет пренебречь. Если затем приложить к кристаллу электрическое поле, то электроны нач­нут двигаться и потечет электрический ток. В принципе они должны очутиться на краю кристалла и, если там имеется ме­таллический электрод, перейти на него, оставив кристалл нейт­ральным.

Точно так же в кристалл можно было бы ввести множество дырок. Они бы начали повсюду бродить как попало. Если при­ложить электрическое поле, то они потекут к отрицательному электроду и затем их можно было бы «снять» с него, что и про­исходит, когда их нейтрализуют электроны с металлического электрода.

Электроны и дырки могут оказаться в кристалле одновре­менно. Если их опять не очень много, то странствовать они будут независимо. В электрическом поле все они будут давать свой вклад в общий ток. По очевидной причине электроны назы­вают отрицательными носителями, а дырки — положитель­ными носителями.

До сих пор мы считали, что электроны внесены в кристалл извне или (для образования дырки) удалены из него. Но можно также «создать» пару электрон—дырка, удалив из нейтрального атома связанный электрон и поместив его в том же кристалле на некотором расстоянии. Тогда у нас получатся свободный электрон и свободная дырка, и движение их будет таким, как мы описали.

Энергия, необходимая для того, чтобы поместить электрон в состояние S (мы говорим: чтобы «создать» состояние S), — это энергия Е - , показанная на фиг. 12.2.

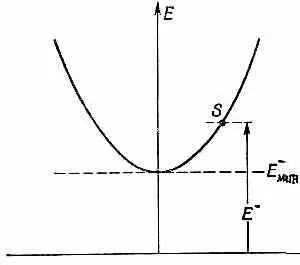
Фиг. 12.2, Энергия Е, требуемая для «рождения» свободного

электрона.

Это некоторая энергия,

превышающая Е - мин . Энергия, необходимая для того, чтобы «создать» дырку в каком-то состоянии S ',— это энергия Е + (фиг. 12.3), которая на какую-то долю выше, чем Е (=Е + мин ).

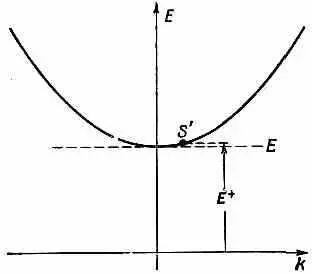
Фиг. 12.3. Энергия Е + , тре­буемая для «рождения» дырки в состоянии S'.

А чтобы создать пару в со­стояниях S и S', потребуется просто энергия Е - + Е + .

Образование пар — это, как мы увидим позже, очень частый процесс, и многие люди предпочитают поме­щать фиг. 12.2 и 12.3 на один чертеж, причем энергию дырок откладывают вниз, хотя, конечно, эта энергия положительна. На фиг. 12.4 мы объединили эти два гра­фика.

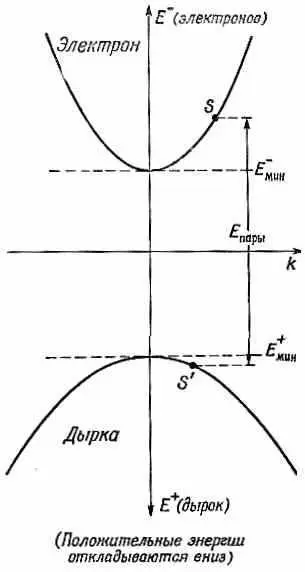
Фиг. 12.4. Энергетические диаграммы для электрона и дырки.

Преимущества такого графика в том, что энергия E пары =Е - +Е + , требуемая для образования пары (электрона в S и дырки в S’ ), дается попросту расстоянием по вертикали между S и S', как показано на фиг. 12.4. Наименьшая энергия, требуемая для образования пары, называется энерге­тической шириной, или шириной щели, и равняется

е - мин +E + мин.

Иногда вам может встретиться и диаграмма попроще. Ее рисуют те, кому не интересна переменная k, называя ее диа­граммой энергетических уровней. Эта диаграмма (она показана на фиг. 12.5) просто указывает допустимые энергии у электро­нов и дырок.

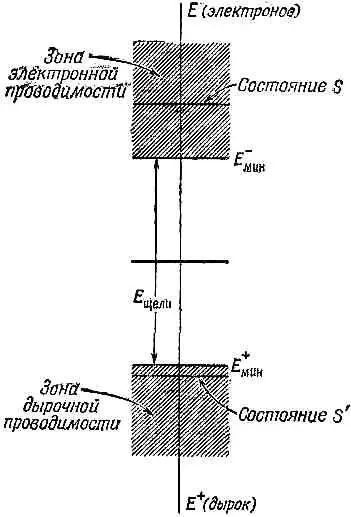
Фиг. 12.5. Диаграмма энер­гетических уровней для электронов и дырок.

Как создается пара электрон—дырка? Есть несколько спо­собов. Например, световые фотоны (или рентгеновские лучи)

могут поглотиться и обра­зовать пару, если только энергия фотона больше энергетической ширины. Быстрота образования пар пропорциональна интен­сивности света. Если при­жать к торцам кристалла два электрода и прило­жить «смещающее» напря­жение, то электроны и дырки притянутся к элек­тродам. Ток в цепи будет пропорционален силе све­та. Этот механизм ответствен за явление фотопроводимости и за работу фотоэлементов. Пары электрон — дырка могут образоваться также части­цами высоких энергий. Когда быстро движущаяся заряженная частица (например, протон или пион с энергией в десятки и сотни Мэв) пролетает сквозь кристалл, ее электрическое поле может вырвать электроны из их связанных состояний, образуя пары электрон — дырка. Подобные явления сотнями и тыся­чами происходят на каждом миллиметре следа. После того как частица пройдет, можно собрать носители и тем самым вызвать электрический импульс. Перед вами механизм того, что разы­грывается в полупроводниковых счетчиках, в последнее время используемых в опытах по ядерной физике. Для таких счетчи­ков полупроводники не нужны, их можно изготовлять и из кристаллических изоляторов. Так и было на самом деле: первый из таких счетчиков был изготовлен из алмаза, который при ком­натных температурах является изолятором. Но нужны очень чистые кристаллы, если мы хотим, чтобы электроны и дырки