Ричард Фейнман - 9. Квантовая механика II

Мы, следовательно, заключаем, что сохранение момен­та количества движения разрешает процесс, показанный на фиг. 15.7, б, но не разрешает процесса, показанного на фиг. 15.7, в. А раз мы знаем, что распад все же про­исходит, то, значит, имеется некоторая амплитуда для процесса, показанного на фиг. 15.7, б, когда протон летит вверх и спин его при этом тоже смотрит вверх. И мы обозначим буквой а амплитуду того, что в бесконечно малый промежуток времени произойдет такой распад.

Теперь посмотрим, что было бы, если бы спин L 0вначале был направлен вниз. Опять рассматриваем распады, в кото­рых протон взлетает вверх по оси z, как показано на фиг. 15.8.

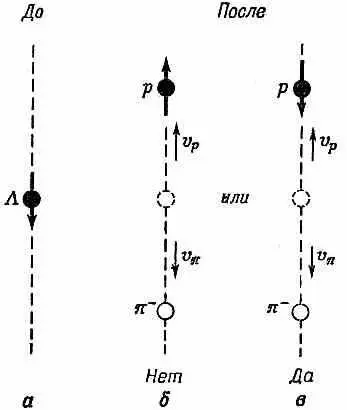
Фиг. 15.8. Распад вдоль оси z для L 0 со спином, направлен­ным вниз.

Вам, конечно, теперь ясно, что в этом случае спин протона направлен вниз (если только момент коли­чества движения сохра­няется). Обозначим ампли­туду такого распада буквой b.

Об амплитудах а и b мы ничего больше сказать не сможем. Они зависят от внутренней механики час­тицы L 0и от слабых распадов, и никто пока не знает, как их подсчитывать. Их приходится полу­чать из опыта. Но, зная только эти две амплитуды, мы можем узнать об угловом распределении распадов все, что захотим. Надо только всегда тщательно и полностью определять те состояния, о которых идет речь.

Мы хотим знать вероят­ность того, что протон вы­летит под углом q к оси z (в некоторый узкий телесный угол qW), как показано на фиг. 15.6. Проведем новую ось z в этом направлении и обозначим ее z'! Как анализировать, что происходит вдоль этой оси, мы знаем. По отношению к ней спин Л° уже не направлен вверх, а имеет какую-то амплитуду того, что он окажется направленным вверх и какую-то — вниз. Все это мы уже подсчитывали в гл. 4, а потом опять в гл. 8 [уравнение (8.30)] (вып. 8). Амплитуда того, что спин будет направлен вверх, есть cosq/2, а амплитуда того, что спин будет смотреть вниз, есть -sinθ/2. Когда спин L 0направлен вверх по оси z', она испустит протон в направлении z с амплиту­дой а. Значит, амплитуда того, что по направлению z пройдет протон, держа свой спин вверх, равна

a cosq/2. (15.33)

Точно так же амплитуда того, что вдоль положительной оси z пройдет протон, направив свой спин вниз, равна

- b sinq/2. (15.34)

Те два процесса, к которым относятся эти амплитуды, показаны

на фиг. 15.9.

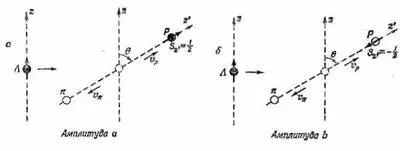
Фиг . 15.9. Два возможных состояния распада L 0 .

Теперь зададим такой немудреный вопрос. Пусть мы соби­раемся регистрировать протоны, вылетающие под углом q, не интересуясь их спином. Два спиновых состояния (вверх и вниз по оси z') различимы, даже если бы мы того и не хотели. Значит, чтобы получить вероятность, надо амплитуды возвысить в квад­рат и сложить. Вероятность f (q) обнаружить протон в неболь­шом телесном угле qW при q равна

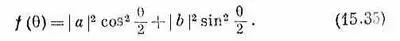
Вспоминая, что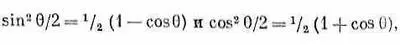

запишем f (q) так:

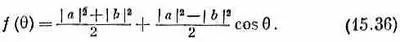
Угловое распределение имеет вид

Одна часть вероятности не зависит от q, а другая зависит от cosq линейно. Из измерений углового распределения мы можем получить a и b, а значит, и | а | , и | b | .

Можно получить ответ и на многие другие вопросы. Может быть, вас интересуют лишь те протоны, спин которых направлен вверх относительно старой оси z? Каждый член в (15.33) и (15.34) даст амплитуду того, что спин протона окажется направ­ленным вверх или вниз по отношению к оси z ' (|+ z '> и |- z '>). А состояние, когда спин направлен вверх относитель­но старой оси, | + z), можно выразить через два базисных со­стояния | + z' > и |-z'>. Можно тогда взять две амплитуды (15.33) и (15.34) с надлежащими коэффициентами (cosq/2 и -sinq/2) и получить полную амплитуду

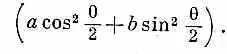
Ее квадрат даст вероятность того, что протон вылетит под углом q со спином, направленным туда же, куда направлен спин L 0(вверх по оси z ).

Если бы четность сохранялась, можно было бы сделать еще одно утверждение. Распад на фиг. 15.8 — это просто зеркальное отражение, скажем в плоскости yz, распада с фиг. 15.7. Если бы четность сохранялась, b равнялось бы либо a , либо - а . Тогда коэффициента в (15.37) был бы равен нулю и распад оди­наково часто происходил бы во всех направлениях.

Результаты опытов говорят, однако, что при распаде асим­метрия существует. Измеренное угловое распределение дейст­вительно, как мы предсказали, меняется по закону cosq, а не по закону cos 2q или по другой степени. Из этого углового распределения, стало быть, следует, что спин L 0равен 1/ 2 . Кроме того, мы видим, что четность не сохраняется. Действи­тельно, коэффициента на опыте найден равным -0,62±0,05, так что b примерно вдвое больше а. Отсутствие симметрии от­носительно отражений совершенно очевидно.

Вы видите, как много можно вывести из сохранения момента количества движения. Еще некоторые примеры будут приведены в следующей главе.

· · ·

Замечание после лекции. Под амплитудой а здесь мы подразумевали амплитуду того, что состояние

| протон летит по + z, спин по + z> обра­зовано за бесконечно малое время dt из состояния |L, спин по + z>, или, иными словами, что

<���протон летит по + z , спин по +z| H |L, спин по + z>= iha, (15.38)

где H — гамильтониан всего мира или по крайней мере той его части, которая ответственна за L-распад. Сохранение момента количества дви­жения означает, что у гамильтониана должно быть такое свойство:

<���протон летит по +z, спин по -z| H |L, спин по +z>=0. (15.39)

Под амплитудой b подразумевается, что

<���протон летит по + z, спин по —z| H |L, спин по -z>= ihb. (15.40)

Сохранение момента количества движения предполагает, что

<���протон летит по + z, спин по + z | H |L , спин по -z>=0. (15.41)

Если вам не ясно, как написаны амплитуды (15.33) и (15.34), можно их записать в более математической форме. Когда мы писали (15.33), нам нужна была амплитуда того, что Л со спином, направленным по +z, распадается на протон, движущийся вдоль направления + z' и обладаю­щий спином, направленным тоже по + z ', т. е.