Ричард Фейнман - 9. Квантовая механика II

Сейчас мы покажем вам, насколько обща эта идея. Применим ее к двум другим законам сохранения, по физической идее точно соответствующим сохранению момента количества движения. В классической физике существует также сохранение импульса и сохранение энергии, и интересно, что оба они тоже связаны с некоторыми физическими симметриями. Положим, у нас имеет­ся физическая система — атом, или сложное ядро, или же моле­кула, или что угодно — и если мы возьмем ее и как целое пере­двинем на новое место, то ничего не изменится. Значит, мы имеем гамильтониан с тем свойством, что он в некотором смысле зави­сит от внутренних координат, но не зависит от абсолютного положения в пространстве. В этих обстоятельствах существует специальная операция симметрии, которая называется простран­ственным переносом. Определим D^ x ( а ) как операцию смещения на расстояние а вдоль оси х. Тогда для каждого состояния мы сможем проделать эту операцию и получить новое состояние. И опять здесь возможны весьма специальные состояния, обла­дающие тем свойством, что когда вы их смещаете по оси х на а, вы получаете то же самое состояние (если не считать фазового множителя). И так же, как делалось выше, можно доказать, что когда так бывает, то фаза пропорциональна а. Так что для этих специальных состояний |y 0> можно писать

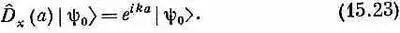
Коэффициент k, умноженный на h , называется х-компонентой импульса. Его называют так потому, что это число, когда система велика, численно совпадает с классическим импульсом р х . Общее утверждение таково: если гамильтониан не меняется при сдвиге системы и если вначале состояние характеризуется опре­деленным импульсом в направлении х, то импульс в направле­нии х останется с течением времени неизменным. Полный им­пульс системы до и после столкновений (или после взрывов или еще чего-нибудь?) будет один и тот же.

Есть и другая операция, которая совершенно аналогична смещению в пространстве: сдвиг во времени. Положим, перед нами физические обстоятельства, когда ничто внешнее от вре­мени не зависит, и вот в этих обстоятельствах мы помещаем нечто в некоторый момент времени в данное состояние и пускаем его на произвол судьбы. А в другой раз (в новом опыте) мы то же самое устройство запускаем двумя секундами позже или вообще т секундами позже. И вот если ничего во внешних условиях не зависит от абсолютного времени, то все будет развиваться точно так же, как прежде, и конечное состояние совпадет с прежним конечным состоянием, за исключением того, что за­поздает на время т. В этих обстоятельствах также найдутся осо­бые состояния, у которых развитие во времени обладает той особенностью, что запоздавшее состояние — это попросту ста­рое состояние, умноженное на фазовый множитель. И на этот раз тоже ясно, что для этих особых состояний изменение фазы должно быть пропорционально t. Можно написать

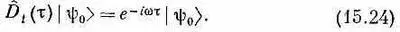
Общепринято при определении w пользоваться знаком минус; при таком соглашении wh — это энергия системы; она сохра­няется. Итак, система с определенной энергией — это такая система, которая при сдвиге во времени на t воспроизводит самое себя, умноженную на e - i w t . (Это как раз то, что мы гово­рили, когда определяли квантовое состояние с определенной энергией, так что все согласуется.) Это означает, что если система находится в состоянии с определенной энергией и если га­мильтониан не зависит от t, то независимо от того, что произой­дет дальше, система во все позднейшие времена будет обладать той же энергией.

Теперь вы понимаете, стало быть, какая связь между законами сохранения и симметрией мира. Симметрия по отношению к сдви­гам во времени влечет за собой сохранение энергии; симметрия относительно положения на осях х, у или z влечет за собой сохранение соответствующей компоненты импульса. Симметрия относительно поворотов вокруг осей х, у и z влечет за собой сохранение х-, у- и z-компонент момента количества движения. Симметрия относительно отражений влечет за собой сохранение четности. Симметрия по отношению к перестановке двух элек­тронов влечет за собой сохранение чего-то, чему не придумано еще названия, и т. д. Часть этих принципов имеет классические аналоги, а часть — нет. В квантовой механике есть больше законов сохранения, чем это нужно для классической механики или по крайней мере чем обыкновенно в ней в ходу.

Чтобы вы смогли разобраться в других книгах по кванто­вой механике, мы сделаем небольшую техническую ремарку и познакомим вас с одним общепринятым обозначением. Операция сдвига по времени — это как раз та самая операция U^, о кото­рой мы как-то говорили:

Многие предпочитают язык бесконечно малых сдвигов по времени или бесконечно малых перемещений в пространстве или пово­ротов на бесконечно малые углы. Поскольку всякое конечное смещение или угол можно постепенно накопить последователь­ными бесконечно малыми смещениями или поворотами, то часто легче проанализировать сначала этот бесконечно малый случай. Оператор бесконечно малого сдвига D t во времени есть (по определению гл. 6, вып. 8)

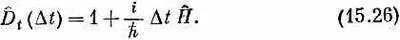
Тогда Н аналогично классической величине, которую мы име­нуем энергией, потому что если Н^ |y> оказывается равным

постоянной, умноженной на |y>, а именно если Н^ |y>= E |y>,

то эта постоянная есть энергия системы.

То же самое проделывается и с другими операциями. Если мы делаем легкое смещение по х, скажем на D x , то состояние

|y>, вообще говоря, перейдет в некоторое новое состояние

|y'>. Мы можем написать

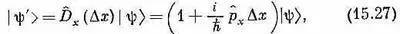
потому что, когда D x стремится к нулю, |y'> обязано обратиться опять в |y>, или, что то же самое, D^ x (0)=1, а для малых D x отклонение D^ x (D x ) от единицы должно быть пропорционально D x . Оператор р х , определенный таким путем, называется оператором импульса (естественно, для x -компоненты).