Ричард Фейнман - 9. Квантовая механика II

|yна 15-й секунде>=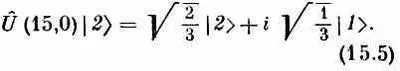

Те же идеи схематично изображены на фиг. 15.2.

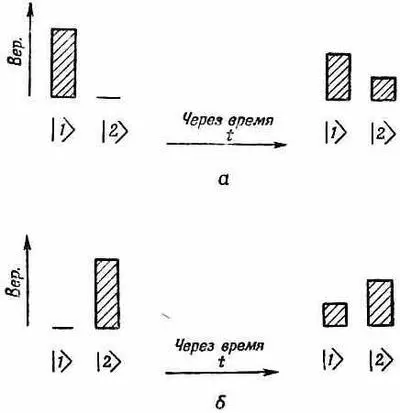
Фиг. 15.2. Если в симметричной системе чистое состояние |1 > развивается во вре­мени так, как показано в части (а), то чистое состояние |2 > будет во времени развиваться так, как показано в части (б).

Итак, если физика системы симметрична относительно некоторой плоскости и мы рассчитали поведение того или иного состояния, то нам также известно поведение состояния, которое получилось бы после отражения исходного состояния в плоскости симметрии.

То же самое можно высказать чуть более общо, т. е. чуть более отвлеченно. Пусть Q^ — любая из множества операций, которые вы можете произвести над системой, не меняя физики. К примеру, за Q^ мы можем принять операцию отражения в пло­скости, расположенной посредине между двумя атомами моле­кулы водорода. Или в системе с двумя электронами можно было бы под Q^ подразумевать операцию обмена двумя электронами. Третьей возможностью явилась бы в сферически симметричной системе операция поворота всей системы на конечный угол вокруг некоторой оси; от этого физика не изменится. Конечно, в каждом отдельном случае мы бы обозначали Q^ по-своему. В частности, через R^ y (q) мы обычно будем обозначать операцию «поверни систему вокруг оси у на угол q». Под Q^ мы просто понимаем один из названных операторов или любой другой, который оставляет всю физическую ситуацию неизменной.

Оператор Q^ мы будем называть оператором симметрии для системы.

Вот вам еще примеры операторов симметрии. Если у нас имеется атом, а внешнее магнитное или внешнее электрическое поле отсутствует, то после поворота системы координат вокруг любой оси физическая система остается той же самой. Опять-таки молекула аммиака симметрична относительно отражения в пло­скости, параллельной той, в которой лежат три атома водорода (пока нет электрического поля). Если есть электрическое поле, то при отражении надо было бы обратить и поле, а это меняет всю физическую задачу. Но пока внешнего поля нет, молекула симметрична.

Теперь рассмотрим общий случай. Положим, мы начали с состояния |y 1>, а через некоторое время или под влиянием других физических условий оно превратилось в состояние |y 2>. Напишем

[Посмотрите на формулу (15.4).] Теперь вообразите, что над всей системой мы проводим операцию Q^. Состояние |y 1> преобра­зится в состояние |y' 1>, которое также записывается в виде Q^| y 1> . А состояние |y 2> превращается в |y' 2>= Q ^|y 2>. И вот, если физика симметрична относительно Q^ (не забывайте про это, если это отнюдь не общее свойство системы), тогда, подождав в тех же условиях то же время, мы должны получить

[Как в (15.5).] Но вместо |y' 1> можно написать Q^ |y 1>, а вместо |y 2> написать Q^ |y 2>, так что (15.7) переписывается в виде

Теперь, если |y 2> заменить на U^ |y 1> [см. (15.6)], то получим

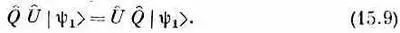
Нетрудно понять, что это значит. В отношении атома водорода это означает, что «отразить и после немного подождать» [правая часть (15.9)] — это то же самое, что «немного подождать, а после отразить» [левая часть (15.9)]. Они должны совпасть, если толь­ко U ^при отражении не меняется.

А поскольку (15.9) справедливо при любом исходном со­стоянии | y 1> , то на самом деле это уравнение для операторов

Это-то мы и хотели получить — математическую формулировку симметрии. Когда соблюдается (15.10), мы говорим, что операторы U^ и Q^ коммутируют. Тогда «симметрию» можно опреде­лить следующим образом: физическая система симметрична относительно операции Q^, когда Q^ коммутирует с U^ (с опера­цией прошествия времени). [На языке матриц произведение двух операторов равнозначно матричному произведению, так что (15.10) в системе, симметричной относительно преобразова­ния Q^, выполняется и для матриц Q^ и U^.]

Кстати, поскольку для бесконечно малого времени 8 мы имеем [7=1 — iH^e/h, где H^ — обычный гамильтониан [см. гл. 6 (вып. 8)1, то легко видеть, что когда (15.10) выполнено, то вы­полнено и

Так что (15.11) есть математическая формулировка условий на симметричность физической ситуации относительно оператора Q^. Она определяет симметрию.

§ 2. Симметрия и ее сохранение

Прежде чем применять только что найденный результат, хотелось бы еще немного вникнуть в идею симметрии. Положим, что стечение обстоятельств таково, что после действия опера­тора Q^ на состояние получается опять то же состояние. Это очень частный случай, но все же допустим, что так сложилось, что состояние |y'>=Q^|y 0>. физически совпадает с состоянием |y 0>. Это значит, что |y'> равняется |y 0>, если не считать не­которого фазового множителя. Как это себе представлять? Пусть, например, имеется ион H + 2в состоянии, которое мы когда-то обозначали | I >. У этого состояния имеется одинаковая ам­плитуда побывать в базисных состояниях | 1 > и | 2 >. Вероят­ности показаны столбиками на фиг. 15.3, а.

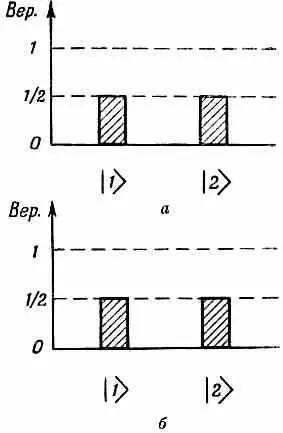
Фиг. 15.3. Состояние | I > и состояние P^ | I >, получае­мые отражением | I > в плоскости, проходящей посреди­не между атомами в ионе Н 2 +.

Если мы на состояние | I > подействуем оператором отраже­ния Р^, он перевернет его, поменяв местами | 1 > с| 2 > , а | 2 > с| 1 >; полу­чатся вероятности, по­казанные на фиг. 15.3,б. Перед нами опять состояние | I >. Если начать с состояния | II >, то вероятности до и после отражения будут выглядеть тоже одинаково. Правда, если посмотреть на ампли­туды, то разница все же есть. У состояния | I > после отраже­ния амплитуды останутся теми же, у состояния | //) они приобретут противоположный знак. Иными словами,