Ричард Фейнман - 9. Квантовая механика II

Следует заметить только одно. Если энергия Е выше верха потенциальной ямы, то дискретных решений уже не будет, и разрешены все мыслимые энергии. Такие решения отвечают рассеянию свободных частиц на потенциальной яме. Пример таких решений мы видели, когда рассматривали влияние атомов примесей в кристалле.

* Помните, еще раньше мы условились, что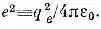

* Был использован тот факт, что 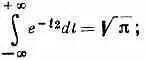см. вып. 1

* О распределениях вероятностей шла речь в гл. 6, § 4 (вып. 1).

* Представьте себе, что по мере сближения точек х n амплитуда А прыжков из х n 1 в х n возрастает.

§ 1. Симметрия

§ 2. Симметрия и ее сохранение

§ 3. Законы сохранения

§ 4. Поляризованный свет

§ 5. Распад Λ°

§ 6. Сводка матриц поворота

Повторить: гл. 52 (вып. 4} «Сим­метрия законов физики»

§ 1. Симметрия

В классической физике немало величин (та­ких, как импульс, энергия и момент количества движения) сохраняется. Теоремы о сохранении соответствующих величин существуют и в кван­товой механике. Самое прекрасное в квантовой механике это то, что теоремы сохранения в опре­деленном смысле удается в ней вывести из чего-то другого; в классической же механике они сами практически являются исходными для других законов. (Можно, правда, и в классиче­ской механике поступать так же, как в кванто­вой, но это удается только на очень высоком уровне.) В квантовой механике, однако, законы сохранения очень тесно связаны с принципом суперпозиции амплитуд и с симметрией физи­ческих систем относительно различных измене­ний. Это и есть тема настоящей лекции. Хотя идеи эти мы будем применять главным образом к сохранению момента количества движения, но существенно здесь то, что все теоремы о сохранении каких угодно величин всегда связа­ны — в квантовой механике — с симметриями системы.

Начнем поэтому с изучения вопроса о симметриях систем. Очень простым примером слу­жат молекулярные ионы водорода (впрочем, в равной степени подошли бы и молекулы ам­миака), у которых имеется по два состояния. У молекулярного иона водорода за одно базис­ное состояние мы принимали такое состояние, когда электрон расположен возле протона № 1, а за другое базисное со­стояние то, в котором электрон располагался возле протона № 2. Эти два состояния (мы их называли | 1 > и | 2 >) мы снова показываем на фиг. 15.1, а.

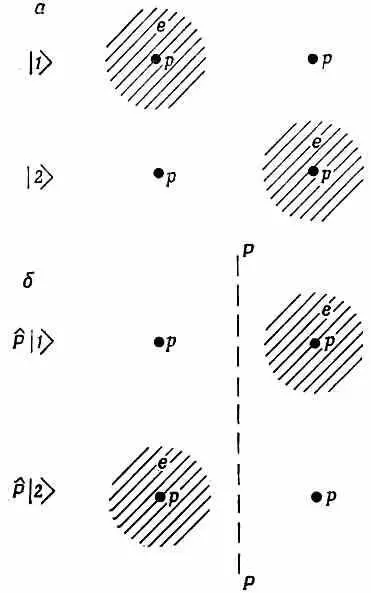
Фиг. 15.1. Если состояния |1> и |2> отразить в плоскости Р—Р, они перейдут соответ­ственно в состояния |2> и |1>.

И вот, по­скольку оба ядра в точ­ности одинаковы, в этой физической системе име­ется определенная сим­метрия. Иначе сказать, если бы нам пришлось отразить систему в пло­скости, поставленной по­средине между двумя протонами (имеется в виду, если бы все находящееся с одной стороны плоскости симметрично перешло на другую сторону), то возникла бы картина, представленная на фиг. 15.1, б. А коль скоро протоны тождественны, операция отражения пе­реводит | 1 >в | 2 >, а | 2> в | 1 >. Обозначим эту операцию отражения Р^ и напишем

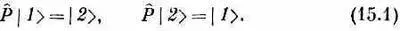
Значит, наше Р^ — это оператор, в том смысле, что он «что-то делает» с состоянием, чтобы вышло новое состояние. Интересно здесь то, что Р^, действуя на любое состояние, создает какое-то другое состояние системы.

Далее, у Р^, как у всякого другого оператора, с которыми мы встречались, есть матричные элементы, которые можно определить с помощью обычных очевидных обозначений. Именно

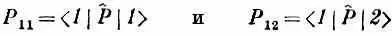
суть матричные элементы, которые получаются, если Р^ |1 > и

Р^|2 >умножить слева на < 1 | . Согласно уравнению (15.1), они равны

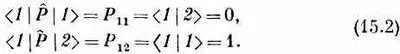
Таким же путем можно получить и Р 21, и Р 22. Матрица Р^ относительно базисной системы|1 > и| 2 > есть

Мы снова убеждаемся, что слова оператор и матрица в кван­товой механике практически взаимозаменяемы. Есть, конечно, легкие технические различия, как между словами «числитель­ное» и «число», но мы не такие педанты, чтобы забивать себе этим голову. Так что будем именовать Р^ то оператором, то мат­рицей, независимо от того, определяет ли оно операцию или реально использовано для получения численной матрицы.

Теперь мы хотели бы кое на что обратить ваше внимание. Предположим, что физика всей системы молекулярного иона водорода сама по себе симметрична. Этого могло бы и не быть — это зависит, например, от того, что находится с нею рядом. Но если система симметрична, то с необходимостью должна быть справедлива следующая идея. Предположим, что вначале, при t= 0 , система находится в состоянии | 1 >, а через промежуток времени t мы обнаруживаем, что система оказалась в более сложном положении — в какой-то линейной комбинации обоих базисных состояний. Вспомните, что в гл. 6 (вып. 8) мы привыкли представлять «эволюцию во времени» умножением на оператор U^. Это означает, что система через мгновение (скажем для опреде­ленности, через 15 сек) окажется в каком-то ином состоянии.

Например, это состояние на Ц 2/ 3может состоять из состояния | 1 > и на i Ц 1/ 3из состояния | 2 >, и мы бы написали

|y на 15-й секунде> = .(15.4)

Теперь спросим: что же произойдет, если вначале мы запустим систему в симметричном состоянии | 2 > и при тех же условиях подождем 15 сек? Ясно, что если мир симметричен (что мы и предполагаем), то обязательно получится состояние, симметрич­ное с (15.4):