Ричард Фейнман - 9. Квантовая механика II

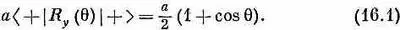
Амплитуда того, что в том же направлении будет испущен ле­вый фотон, равна произведению - а на амплитуду того, что в новом направлении будет m =-1. Из табл. 15.2 следует

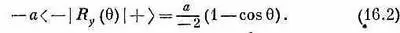
Если вас интересуют другие поляризации, то их амплитуды вы получите из суперпозиции этих двух амплитуд. Чтобы получить интенсивность любой компоненты как функцию угла, вам при­дется, конечно, взять квадрат модуля амплитуд.

§ 2. Рассеяние света

Воспользуемся этими результатами, чтобы решить немного более сложную задачу, но зато и более близкую к реальности. Предположим, что те же атомы находятся в своем основном со­стоянии ( j =0) и рассеивают падающий на них пучок света. Пусть свет первоначально распространяется в направлении + z, так что фотоны падают на атом из направления - z, как показано на фиг. 16.4, а.

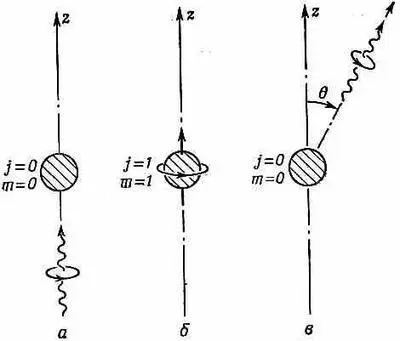
Фиг. 16.4. Рассеяние света атомом, рас­сматриваемое как процесс, состоящий из двух шагов.

Рассеяние света мы можем рассматри­вать как процесс, состоящий из двух шагов: фотон поглощается, а затем вновь излучается. Если мы начнем с правого фотона (фиг. 16.4, а ) и если момент количества движения сохраняется, то после поглощения атом окажется в состоянии с m= +1 (фиг. 16.4, б). Амплитуду этого процесса мы обозначим с. Затем атом может испустить правый фотон в направлении q (фиг.16.4, в ). Полная амплитуда того, что правый фотон рассеется в на­правлении q, равна просто произведению с на (16.1). Обозначая эту амплитуду рассеяния < R ' | S | R > , имеем

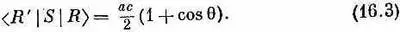
Имеется также амплитуда того, что поглотится правый фотон, а излучится левый. Произведение обеих амплитуд — это амплитуда S | R > — амплитуда того, что правый фотон, рассеявшись, превратится в левый. Используя (16.2), имеем

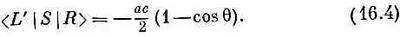
Теперь посмотрим, что происходит, если на атом падает левый фотон. Когда он поглощается, сам атом переходит в со­стояние с m =-1. Рассуждая так же, как в предыдущем па­раграфе, можно показать, что эта амплитуда будет равна - с. Амплитуда того, что атом в состоянии с m =-1 испустит правый фотон под углом q, равна произведению а на амплитуду <+| R y (q)| —>, равную 1/ 2(1- cosq). В итоге получается

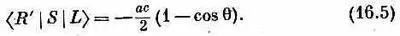
Наконец, амплитуда того, что левый фотон после рассеяния останется левым, есть

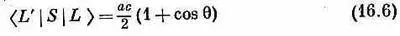
(здесь минус на минус дал плюс).

Если мы измеряем интенсивность рассеяния для любой дан­ной комбинации круговых поляризаций, то она будет пропор­циональна квадрату одной из этих четырех амплитуд. Например, если падает правополяризованный пучок света, то интенсивность правополяризованного света в рассеянном излучении будет меняться как (1 + cosq) 2.

Все это прекрасно, но допустим, что мы хотели бы начать с линейно поляризованного света. Чего можно было бы тогда ожидать? Если свет поляризован вдоль оси х, его можно пред­ставить как суперпозицию право- и левополяризованного по кругу света. Мы пишем [см. гл. 9, § 4 (вып. 8)]

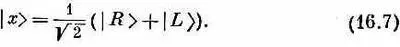
Или если свет поляризован вдоль оси у, то

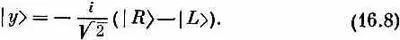
Ч то вы теперь хотите знать? Хотите знать амплитуду того, что х- поляризованный фотон рассеется под углом в как правый фотон? Пожалуйста. Примените для этого обычное правило комбинирования амплитуд. Сначала умножьте (16.7) на < R '| S. Вы получите

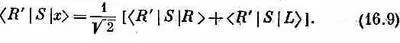
Теперь подставьте сюда (16.3) и (16.5). Получается

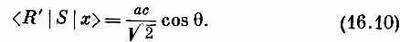
Если бы вам нужна была амплитуда того, что x-фотон рассеется как левый фотон, то вы бы получили

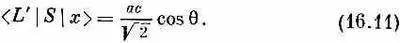
Наконец, представим, что вас заинтересовала амплитуда того, что x -поляризованный фотон рассеется, сохранив свою x -поляризацию. Значит, вам нужно знать <���х'| S | х > . Это мож­но записать так:

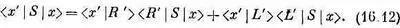
Если вы затем вспомните соотношения

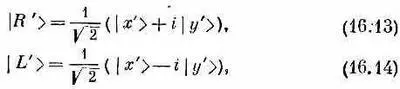
то из них последует

В итоге вы получите

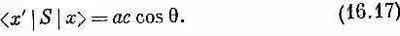
Ответ, стало быть, состоит в том, что пучок x -поляризованного света рассеивается в направлении q (в плоскости xz) с интен­сивностью, пропорциональной cos 2q. Если же нас интересует y -поляризованный свет, то

Иначе говоря, рассеянный свет полностью поляризован в x -направлении.

Здесь отметим интересную вещь. Формулы (16.17) и (16.18) точно соответствуют классической теории рассеяния света, которую мы излагали в гл. 32, § 5 (вып. 3), считая, что электрон связан с атомом линейной возвращающей силой, что действует он как классический осциллятор. Вы можете подумать: «А в классической теории все было куда проще; если она дает верный ответ, зачем забивать себе голову квантовой теорией?» Во-пер­вых, мы пока рассмотрели только один частный (хотя и частый) случай атома с возбужденным состоянием j =1 и с основным состоянием j =0. Если бы возбужденное состояние имело спин, равный 2, вы бы получили уже иные результаты. Во-вторых, нет причины, почему бы модель электрона, привязанного к пружинке и приводимого в движение колеблющимся электриче­ским полем, должна была бы быть верна для одиночного фотона. Правда, мы обнаружили, что она все же верна и что интен­сивность и поляризация оказываются какими надо. Так что в каком-то смысле мы в течение нашего курса лавировали где-то неподалеку от истины. В начале курса мы излагали теорию показателя преломления и рассеяния света, опираясь на клас­сические представления. А теперь мы показали, что квантовая теория в самых обычных случаях приводит к тому же результату. Мы фактически только что объяснили такое, скажем, явление, как поляризация дневного света, с помощью квантовомеханических рассуждений, а это единственный по-настоящему закон­ный путь.