Ричард Фейнман - 9. Квантовая механика II

Вообще все имеющие сегодня хождение классические теории должны быть в конечном счете подтверждены единственно пра­вильными квантовыми аргументами. Естественно, что все те вещи, на объяснения которых мы потратили прежде столько времени, были отобраны как раз из тех частей классической физики, которые еще подтверждаются квантовой механикой. Заметьте, что мы не обсуждали во всех деталях такие модели атома, в которых электроны двигались вокруг ядра по орбитам. Это потому, что такая модель не дает результатов, согласуемых с квантовой механикой. Но электрон на пружинке (хоть эта картина ничуть не смахивает на настоящий атом) действительно с ней согласуется, и потому мы применяли эту модель в теории показателя преломления.

§ 3. Аннигиляция позитрония

Теперь хотелось бы рассмотреть еще один очень интересный пример. Он очень привлекателен, хотя и немного сложен, но, надеемся, все же не слишком. Пример этот — система, именуе­мая позитронием, т. е. «атом», составленный из электрона и позитрона,— связанное состояние е + и е - . Он походит на атом водорода, только вместо протона стоит позитрон. Как и у водо­рода, у него много состояний. И как у водорода, основное со­стояние вследствие взаимодействия с магнитным моментом рас­щепляется на «сверхтонкую структуру». Спины электрона и позитрона равны 1/ 2и могут быть либо параллельны, либо антипараллельны любой данной оси. (В основном состоянии орбитальное движение не создает своего момента количества движения.) Итак, всего есть четверка состояний: три из них — подсостояния системы со спином 1, все с одной энергией; и одно состояние со спином нуль и с иной, отличной энергией. Однако расщепление уровней здесь намного сильнее, чем те 1420 Мгц, которые есть в спектре водорода, потому что маг­нитный момент у позитрона куда больше протонного — в 1000 раз.

Но самое важное различие в том, что позитроний не может существовать вечно. Позитрон — это античастица электрона; они могут взаимно друг друга уничтожить. Две частицы полно­стью исчезают, обращая свою энергию покоя в излучение в виде g-квантов (фотонов). Две частицы с конечной массой покоя переходят в пару (а то и больше) объектов с нулевой массой покоя.

Начнем с анализа распада состояния позитрония со спином нуль. Он распадается на два g-кванта со временем жизни 10 -1 0 сек. Вначале имеются позитрон и электрон с антипараллельными спинами, расположенные очень близко один к другому и образующие систему позитрония. После распада возникают два фотона, разлетающиеся с равными и противоположными импульсами (фиг. 16.5).

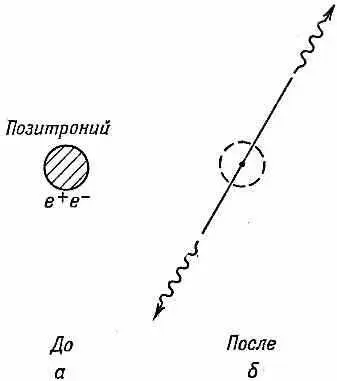
Фиг. 16.5. Двухфотонная аннигиляция позитрония.

Импульсы обязаны быть равны и про­тивоположны, потому что полный импульс после распада дол­жен быть таким, как и до распада, т. е. равен нулю (если мы рас­сматриваем аннигиляцию в покое). Если позитроний движется, мы можем нагнать его, решить задачу и затем все преобразовать обратно в лабораторную систему (вот видите — мы теперь все умеем; все, что надо, у нас под рукой).

Для начала заметим, что угловое распределение интереса не представляет. Раз спин начального состояния равен нулю, то нет какой-либо выделенной оси, оно симметрично относи­тельно любых поворотов. Значит, и конечное состояние должно быть симметрично относительно всякого поворота. Это означает, что все углы распада одинаково вероятны — амплитуда выле­теть в любую сторону для фотона одна и та же. Конечно, если один из фотонов отправляется в одну сторону, то другой отпра­вится в противоположную.

Единственное, что нам остается, это рассмотреть поляриза­цию фотонов. Проведем ось +z по направлению движения од­ного фотона, а ось - z по направлению движения второго фотона. Для описания состояний поляризации фотонов можно использовать любые представления. Мы выберем правую и левую круговые поляризации, всегда отсчитывая их относитель­но направлений движения. Сразу же видно, что если движущийся вверх фотон — правый, то момент количества движения оста­нется прежним, если фотон, отправившийся вниз, тоже окажется правым. Каждый унесет по +1 единице момента относительно направления своего импуль­са, что означает +1 и -1 относительно оси z. В сумме будет нуль, и мо­мент количества движения после распада окажется та­ким же, как и до распада (фиг. 16.6).

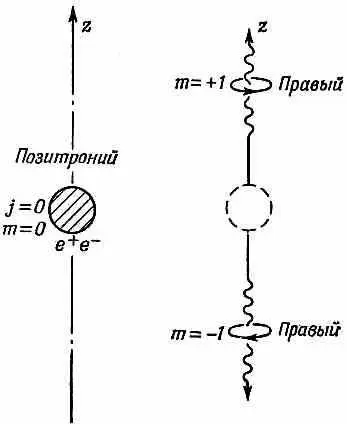
Фиг. 16.6. Одна из возмож­ностей для аннигиляции пози­трония вдоль оси z.

Те же рассуждения по­казывают, что если движущийся вверх фотон является правым, то движущийся вниз не может быть левым, ведь тогда конечное состояние обла­дало бы двумя единицами момента количества движения. А это не разрешается, если спин начального состояния равен нулю. Заметьте, что такое конечное состояние невозможно и тогда, когда основное состояние позитрония обладает спином 1, потому что в этом случае наибольшая величина момента количества движения в любом направлении равна единице.

А теперь мы покажем, что двухфотонная аннигиляция из состояния со спином 1 вообще невозможна. Могло бы показать­ся, что это не так, что если взять состояние с j =1, m =0, у которого момент количества движения относительно оси z равен нулю, то оно будет походить на состояние со спином 0 и поэтому распадется на два правых фотона. Конечно, изображен­ный на фиг. 16.7, а распад сохраняет момент количества движе­ния относительно оси z.

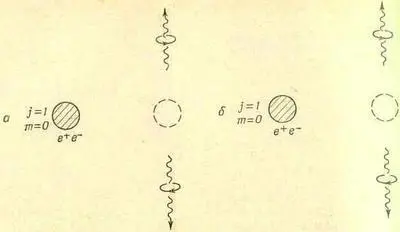
Фиг. 16.7. Для состояния позитрония с j = 1 процесс (а) и процесс (б), получаемый поворотом (а) вокруг оси у на 180°, в точности совпадают.

Но посмотрим, что будет, если мы повернем эту систему вокруг оси у на 180°; получится то, что показано на фиг. 16.7, б, т. е. конфигурация, в точности сов­падающая с фиг. 16.7, а. Обменялись местами два фотона и больше ничего. А ведь фотоны — это бозе-частицы; перестановка их местами не меняет знака амплитуды, так что амплитуда распада на конфигурацию, показанную на фиг. 16.7, б, должна быть такой же, как и на конфигурацию фиг, 16.7, а. Но мы предполо­жили, что у начального объекта спин был равен единице. А когда мы поворачиваем объект со спином 1 в состоянии с m =0 на 180° вокруг оси у, то его амплитуда меняет знак (см. табл. 15.2 для q=p, стр. 129). Значит, амплитуды обеих конфигура­ций на фиг. 16.7 должны иметь обратные знаки; частица со спи­ном 1 не может распадаться на два фотона.