Ричард Фейнман - 9. Квантовая механика II

состояние | 0, 0>.

Теперь мы можем посмотреть, что происходит, когда мы прое­цируем общее состояние | j, m >на представление, относящееся к повернутой системе осей. Прежде всего известно, что j — это число, которое характеризует систему, поэтому оно не меняется. При повороте осей мы получим просто смесь различных значе­ний т для одного и того же j . В общем случае появится амплиту­да того, что система в повернутой системе координат окажется в состоянии | j , m' > , где m' — новая z-компонента момента ко­личества движения. Значит, нам нужны матричные элементы < j , m' | R | j, m >всевозможных поворотов. Мы уже знаем, что бывает, если поворот делается на угол j вокруг оси z. Новое состояние — это попросту старое, умноженное на e im j , у него по-прежнему то же значение т. Это можно записать так:

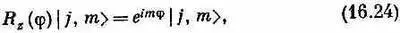
или, если вам больше нравится,

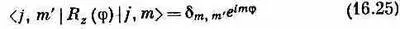
(где d m , m 'равно единице при m' = m, и нулю в прочих случаях).

При поворотах вокруг любой другой оси возникает переме­шивание различных m -состояний. Можно было бы, конечно, попытаться подсчитать матричные элементы для произвольных поворотов, описываемых углами Эйлера b,a и g . Но будет легче, если мы вспомним, что самый общий такой поворот может быть составлен из трех поворотов R z (g), R y (a), R z (b); так что если мы знаем матричные элементы для поворотов вокруг оси y , то уже располагаем всем необходимым.

Как же нам найти матрицу поворота для поворота частицы со спином j на угол q вокруг оси у? Опираясь на основные за­коны (и на то, что уже было), это сделать нелегко. Мы так посту­пали со спином 1/ 2: вывели все, что нужно, пользуясь довольно сложными соображениями симметрии. Для спина 1 мы это про­делали уже иначе: рассмотрели частный случай, когда система со спином 1 складывается из двух систем со спином 1/ 2. Если вы последуете за нами и признаете правильным тот факт, что в общем случае ответы зависят только от спина j , а не от того, как скреплены между собой разные части системы со спином j , то мы сможем обобщить рассуждения для спина 1 на произвольный спин. Мы сможем, например, соорудить искусственную систему со спином 3/ 2из трех объектов со спином 1/ 2. Мы сможем даже избежать всяких усложнений, вообразив, что все они суть различные частицы — скажем, протон, электрон и мюон. Преобразуя каждый объект со спином 1/ 2, мы увидим, что происходит со всей системой — надо только вспомнить, что для комбинированного состояния все амплитуды перемножаются. Давайте посмотрим, как все это проходит.

Допустим, мы расположили все три объекта со спином 1/ 2спинами вверх; обозначим такое состояние |+++>. Если мы взглянем на него из системы координат, повернутой относительно оси z на угол j, то каждый плюс останется плюсом, но умно­жится на е i j /2 . Таких множителей у нас тройка, так что

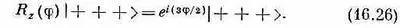
Ясно, что состояние |+++> — это как раз то, что мы назы­ваем состоянием m =+ 3/ 2, или состоянием | 3/ 2, + 3/ 2>.

Если мы затем повернем эту систему вокруг оси у, то у каж­дого из объектов со спином 1/ 2появится некоторая амплиту­да стать плюсом или стать минусом, так что вся система станет теперь смесью восьми возможных комбинаций |+++>,

|++->, |+-+>, |-++>, |+-->, |-+->,

|--+> или |---> . Ясно, однако, что их можно раз­бить на четыре группы, чтобы каждая соответствовала своему значению m. Прежде всего мы имеем |+++>, для которого m = 3/ 2. Затем имеется тройка состояний |++->, |+-+> и |-++> — каждое с двумя плюсами и одним минусом. Поскольку каждый из объектов со спином 1/ 2имеет равные шансы стать после поворота минусом, то каждая из этих трех комбинаций должна войти на равных паях. Поэто­му возьмем комбинацию

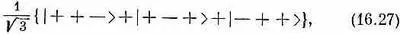
где множитель 1/Ц3 поставлен для нормировки. Если мы по­вернем это состояние вокруг оси z, то получим множитель e i j /2 для каждого плюса и e - i f /2 для каждого минуса. Каждое слагаемое в (16.27) умножится на e i j /2 , и общий множитель е i j / 2 мы вынесем за скобки. Такое состояние соответствует нашему представлению о состоянии с m= + 1/ 2; мы приходим к выводу, что

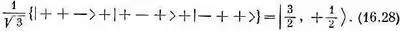
Точно так же можно написать

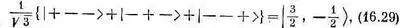
что соответствует состоянию с m=- 1/ 2. Заметьте, что мы берем только симметричные сочетания, у нас нет комбинаций, куда входят слагаемые со знаком минус. Они отвечали бы со­стояниям с таким же т, но с иным j . Это аналогично случаю спина 1, где (1/Ц2){|+->+|-+>} было состоянием | 1,0>, а (1/Ц2){|+->-|-+>} было состоянием | 0,0>. Наконец, мы имеем

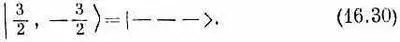
Эта четверка состояний сведена в табл. 16.1.

Таблица 16.1 · СВОДКА СОСТОЯНИЙ

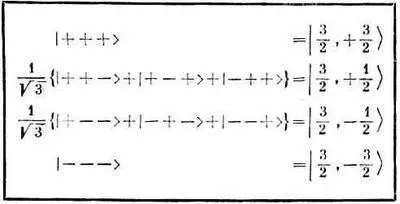
Все, что нам теперь нужно сделать, это взять каждое состоя­ние, повернуть его вокруг оси у и посмотреть, сколько новых состояний оно создаст — пользуясь известной нам матрицей поворота для частицы спина 1/ 2. Можно поступать так же, как мы это делали в случае спина 1 [см. гл. 10, § 6 (вып. 8)]. (Только алгебры будет побольше.) Мы будем строго следовать идеям гл. 10 (вып. 8), так что подробных объяснений давать не будем. Состояния в системе S будут обозначаться

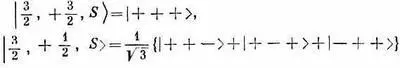
и т. д.; T -системой будет считаться система, повернутая вокруг оси у системы S на угол q. Состояния в T -системе будут обозна­чаться | 3/ 2, + 3/ 2, Т > , | 3/ 2, + 1/ 2, Т >и т. д. Ясно, что | 3/ 2, + 3/ 2, Т >это то же самое, что | +' + ' + ' > (штрихи всегда относятся к T -системе). Точно так же | 3/ 2, + 1/ 2, Т >будет равняться