Ричард Фейнман - 9. Квантовая механика II

Пользуясь состояниями из этой таблицы, мы хотим образо­вать четверку состояний с J = 3/ 2. Но ответ нам уже известен, потому что в табл. 16.1 уже стоят состояния со спином 3/ 2, образованные из трех частиц со спином 1/ 2. Первое состояние в табл. 16.1 имеет | J = 3/ 2, М =+ 3/ 2>, это |+++>, а в наших нынешних обозначениях это | e, + 1/ 2; n, + 1/ 2; p, + 1/ 2>, или первое состояние из табл. 16.4. Но это состояние — то же самое, что первое по списку в (16.42), так что наше выражение (16.45) подтверждается. Вторая строчка в табл. 16.1 утверждает, если воспользоваться нашими теперешними обозначениями, что

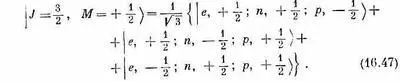
То, что стоит в правой части, можно, очевидно, составить из двух членов во второй строчке табл. 16.4, взяв Ц 2/ 3от пер­вого члена и Ц 1/ 3от второго. Иначе говоря, (16.47) эквива­лентно

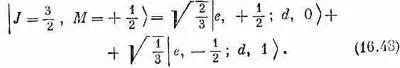
Таблица 16.4 · СОСТОЯНИЯ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ АТОМА ДЕЙТЕРИЯ

Мы нашли два наших первых коэффициента Клебша — Гор­дона a , и b [см. (16.46)]:

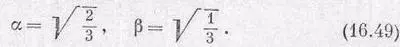
Повторяя ту же процедуру, найдем

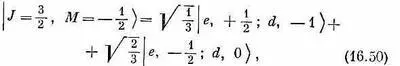
а также, конечно,

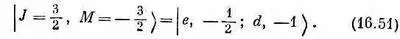
Это и есть правила составления из спина 1 и спина 1/ 2полного спина J = 3/ 2. Мы свели (16.45) и (16.50) в табл. 16.5.

Таблица 16.5 · СОСТОЯНИЯ С J = 3/ 2АТОМА ДЕЙТЕРИЯ

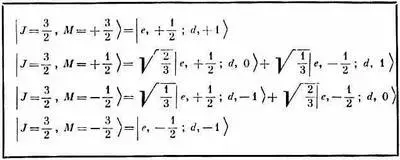
Но у нас пока есть только четыре состояния, а у системы, которую мы рассматриваем, их шесть.

Из двух состояний во второй строчке (16.42) мы для об­разования | J = 3/ 2, М =+ 1/ 2> составили только одну линей­ную комбинацию. Есть и другая линейная комбинация, орто­гональная к ней, у нее тоже М =+ 1/ 2и она имеет вид

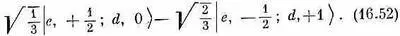
Точно так же из двух состояний в третьей строке (16.42) можно скомбинировать два взаимно-ортогональных состояния, каждое с М =- 1/ 2. То, которое ортогонально к (16.50), имеет вид

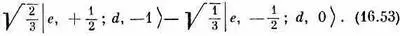
это и есть два оставшихся состояния. У них M=m e +m d = ± 1/ 2; эти состояния должны соответствовать J = 1/ 2. Итак, мы имеем

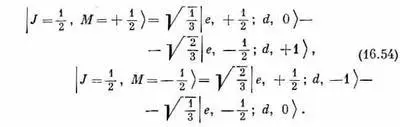
Можно убедиться, что эти два состояния действительно ведут себя как состояния объекта со спином 1/ 2; для этого надо выразить дейтронную часть через нейтронные и протонные со­стояния (при помощи табл. 16.3). Первое состояние в (16.53) превратится в

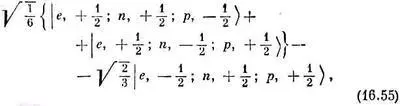
(16.55) а это можно переписать так:

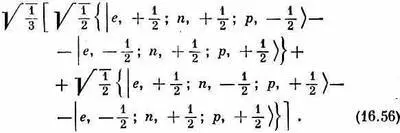
Посмотрите теперь на выражение в первых фигурных скобках и подумайте, что получается при объединении е и р. Вместе они образуют состояние с нулевым спином (см. нижнюю строку в табл. 16.3) и не дают вклада в момент количества движения. Остался только нейтрон, значит, вся первая фигурная скобка (16.56) будет вести себя при поворотах как нейтрон, а именно как состояние с J= 1/ 2 , M=+ 1/ 2.

Повторяя те же рассуждения, убедимся, что во вторых фигурных скобках (16.56) электрон и нейтрон объединяются, чтобы образовать нулевой момент количества движения, и ос­тается только вклад протона — с m p =+ 1/ 2. Скобка опять ведет себя как объект с J =+ 1/ 2, М =+ 1/ 2. Значит, и все выра­жение (16.56) преобразуется как | J =+ 1/ 2, М =+ 1/ 2>, чего мы и хотели. Состояние М= - 1/ 2,отвечающее формуле (16.56), можно расписать так (заменив везде, где нужно, + 1/ 2на - 1/ 2):

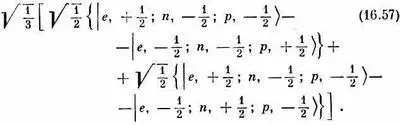
Вы легко проверите, что это совпадает со второй строчкой в (16.54), как и полагается, если каждая скобка представляет собой одно из двух состояний системы со спином 1/ 2. Значит, наши результаты подтвердились. Дейтрон и электрон могут существовать в шести спиновых состояниях, четыре из которых ведут себя как состояния объекта со спином 3/ 2(табл. 16.5), а два — как объект со спином J/ 2(16.54).

Результаты табл. 16.5 и уравнения (16.54) мы получили, вос­пользовавшись тем, что дейтрон состоит из нейтрона и протона. Правильность уравнений не зависит от этого особого обстоятель­ства. Для любого объекта со спином 1, объединяемого с объектом со спином 1/ 2, законы объединения (и коэффициенты) одни и те же. Совокупность уравнений в табл. 16.5 означает, что если система координат поворачивается, скажем, вокруг оси у, так что состояния частицы со спином 1 / 2и частицы со спином 1 изме­няются согласно табл. 16.1 и 16.2, то линейные комбинации по правую сторону знака равенства будут изменяться так, как это свойственно объекту со спином 3/ 2. При таком же повороте со­стояния (16.54) будут меняться как состояния объекта со спи­ном 1/ 2. Результаты зависят только от свойств относительно пово­ротов (т. е. от спиновых состояний) двух исходных частиц, но отнюдь не от происхождения их моментов количества движения. Мы этим происхождением воспользовались лишь для вывода формул, выбрав частный случай, в котором одна из составных частей сама состоит из двух частиц со спином 1/ 2в симметричном состоянии. Все наши результаты мы свели в табл. 16.6, изменив индексы е и d на а и b, чтобы подчеркнуть их общность.

Таблица 16.6 · ОБЪЕДИНЕНИЕ ЧАСТИЦЫ СО СПИНОМ 1/ 2( j a= 1/ 2) С ЧАСТИЦЕЙ СО СПИНОМ 1 ( j b =1)

Поставим теперь себе общую задачу найти состояния, кото­рые можно образовать, объединяя два объекта с произвольными спинами. Скажем, у одного спин j a (так что его z -компонента m а пробегает 2 j а +1 значений от - j a до + j a , а у другого j b (с z-компонентой m b , пробегающей значения от - j b до+ j b ).