Ричард Фейнман - 9. Квантовая механика II

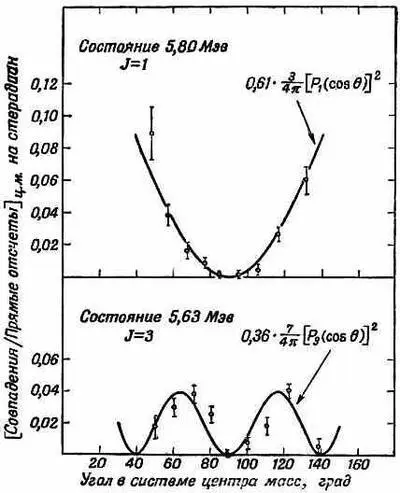
Фиг. 16.10. Экспе­риментальные резуль­таты измерений уг­лового распределения a-частиц, вылетающих при распаде двух воз­бужденных состояний Ne 20 .

Они получены на устрой­стве, показанном на фиг. 16.9.

Вы видите, что угловое распределение для состояния 5,80 Мэв очень хорошо укладывается на кривую [Р 1(cosq)] 2, т. е. оно должно быть состоянием со спином 1. С другой стороны, данные для состоя­ния 5,63 Мэв выглядят совершенно иначе; они ложатся на кривую [ Р 3(cosq)] 2. Спин этого состояния равен 3.

В этом опыте мы измерили момент количества движения двух возбужденных состояний Ne 20*. Этой информацией можно воспользоваться, чтобы понять, как ведут себя протоны и нейтроны внутри этого ядра, и это принесет нам добавочные сведения о таинственных ядерных силах.

§ 6. Сложение моментов количества движения

Когда мы изучали сверхтонкую структуру атома водорода в гл. 10 (вып. 8), нам пришлось рассчитывать внутренние состоя­ния системы, составленной из двух частиц — электрона и протона — со спинами 1/ 2. Мы нашли, что четверка возможных спиновых состояний такой системы может быть разбита на две группы — на тройку состояний с одной энергией, которая во внешнем поле выглядела как частица со спином 1, и на одно ос­тавшееся состояние, которое вело себя как частица со спином 0. Иначе говоря, объединяя две частицы со спином 1/ 2, можно образовать систему, «полный спин» которой равен либо единице, либо нулю. В этом параграфе мы хотим рассмотреть на более общем уровне спиновые состояния системы, составленной из двух частиц с произвольными спинами. Это другая важная проблема, связанная с моментами количества движения квантовомеханической системы.

Перепишем сперва результаты гл. 10 для атома водорода в форме, которая позволит распространить их на более общий случай. Мы начали с двух частиц, которые теперь обозначим так: частица а (электрон) и частица b (протон). Спин частицы а был равен j a (= 1/ 2), a z-компонента момента количества движе­ния m а могла принимать одно из нескольких значений (на са­мом деле два, а именно m а =+ 1/ 2или m а =- 1 / 2). Точно так же спиновое состояние частицы b описывалось ее спином j b и z-компонентой момента количества движения m b . Из всего этого можно было составить несколько комбинаций спиновых состояний двух частиц. Например, из частицы а с m а = 1/ 2и частицы b с m b =- 1/ 2можно было образовать состояние | а, + 1/ 2; b, - 1/ 2>. Вообще, объединенные состояния образовы­вали систему, у которой «спин системы», или «полный спин», или «полный момент количества движения» J мог быть равен либо единице, либо нулю, а z-компонента момента количества движения М могла равняться +1, 0 или -1 при J =1 и нулю при J =0. На этом новом языке формулы (10.41) и (10.42) можно переписать так, как показано в табл. 16.3.

Левый столбец таблицы описывает составное состояние через его полный момент количества движения J и z -компоненту М.

Таблица 16.3 · СОСТАВЛЕНИЕ МОМЕНТОВ КОЛИЧЕСТВА ДВИЖЕНИЯ ДВУХ ЧАСТИЦ СО СПИНОМ 1/ 2,

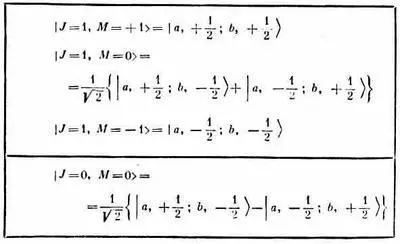
Правый столбец показывает, как составляются эти состояния из значений т двух частиц а и b.

Мы хотим обобщить этот результат на состояния, составлен­ные из двух объектов а и b с произвольными спинами j а и j b . Начнем с разбора примера, когда j а = 1/ 2и j b =1, а именно с атома дейтерия, в котором частица а — это электрон е, а части­ца b — ядро, т. е. дейтрон d. Тогда j a = j e = 1 / 2. Дейтрон обра­зован из одного протона и одного нейтрона в состоянии с пол­ным спином 1, так что j b =j d = 1. Мы хотим рассмотреть сверхтонкие состояния дейтерия, как мы сделали это для водо­рода. Поскольку у дейтрона может быть три состояния, m b = m d =+1, 0, -1, а у электрона — два, m а = m е =+ 1/ 2, - 1/ 2, то всего имеется шесть возможных состояний, а именно (используется обозначение

| е, m e ; d, m d >):

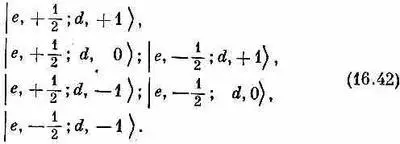
Обратите внимание, что мы разверстали состояния согласно значениям суммы m e и m d в порядке ее убывания.

Спросим теперь: что случится с этими состояниями, если спроецировать их в другую систему координат? Если эту новую систему просто повернуть вокруг оси z на угол j, то состояние | е, m e ; d, m d >умножается на

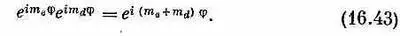
(Состояние можно считать произведением | е, m е >| d, m d >, и каждый вектор состояния независимо привнесет свой собст­венный экспоненциальный множитель.) Множитель (16.43) имеет форму е iM j , поэтому z-компонента момента количества движения у состояния | е, m е ; d, m d >окажется равной

M=m e +m d . (16.44)

Иначе говоря, z-компонента полного момента количества движения есть сумма z-компонент моментов количества движе­ния отдельных частей.

Значит, в перечне состояний (16.42) верхнее состояние имеет М =+ 3/ 2, Два следующих М =+ 1/ 2, затем два М =- 1/ 2и последнее состояние М=- 3/ 2. Мы сразу же видим, что одной из возможностей для спина J объединенного состояния (для полного момента количества движения) должно быть 3/ 2, это потребует четырех состояний с М= + 3/ 2, + 1/ 2 , - 1/ 2и - 3/ 2. На М=+ 3/ 2есть только один кандидат, и мы сразу видим, что

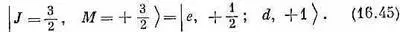
Но что является состоянием | J = 3/ 2, М =+ 1/ 2>? Кандидатов здесь два, они стоят во второй строчке (16.42), и всякая их ли­нейная комбинация тоже даст М= + 1/ 2 . Значит, в общем случае можно ожидать, что

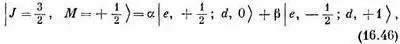
где a и b — два числа. Их именуют коэффициенты Клебша — Гордона. Найти их и будет нашей очередной задачей.

И мы их легко найдем, если просто вспомним, что дейтрон состоит из нейтрона и протона, и в явном виде распишем со­стояния дейтрона, пользуясь правилами табл. 16.3. Если это проделать, то перечисленные в (16.42) состояния будут выгля­деть так, как показано в табл. 16.4.