Ричард Фейнман - 9. Квантовая механика II

Объединенные состояния суть | а, m а ; b, m b > , их всего (2 j a +1)(2 j b +1). Какие же состояния с полным спином / мы обнаружим?

Полная z-компонента М момента количества движения рав­няется m а +m b , и все состояния можно перечислить, опираясь на величину М [как в (16.42)]. Наибольшое М является единст­венным; оно отвечает значениям m a =j a и m b =j b и равно по­просту j a +j b . Это означает, что наибольший полный спин J также равен сумме j а +j b :

J = М макс= j a +j b .

Следующему значению М, меньшему чем М максна единицу, будут соответствовать два состояния (либо m а , либо m b меньше своих максимальных значений на единицу). Из них должно быть образовано одно состояние, принадлежащее совокупности с J=j a +j b , и останется еще одно, которое будет принадлежать новой совокупности с J=j a +j b - 1. Следующее значение М (третье сверху) можно составить тремя путями (из m a =j a — 2, m b = j b , из m a =j a - 1, m b =j b - 1 и из m a =j a , m b =j b - 2). Два из них принадлежат к уже начавшим составляться груп­пам; третье говорит нам, что надо включить в рассмотрение и со­стояния с J=j a +j b -2. Такие рассуждения будут продол­жаться до тех пор, пока уже нельзя будет, меняя то одно, то дру­гое т, получать новые состояния.

Пусть из j а и j b меньшим является j b (а если они одинаковы, возьмите любое из них); тогда понадобятся только 2 j b значений полного спина J , идущих единичными шагами от j а +j b вниз к j а -j b . Иначе говоря, когда объединяются два объекта со спинами j а и j b , то полный момент количества движения J их системы может равняться одному из значений:

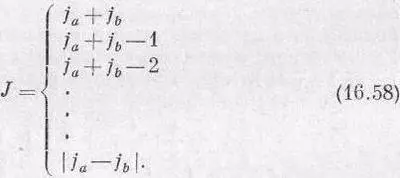
(Написав | j a -j b |вместо j a -j b , мы можем избежать напо­минания о том, что j a іj b .)

Для каждого из этих значений J имеется 2J+1 состояний с различными значениями М; М меняется от + J до - J . Каждое из них образовано из линейных комбинаций исходных состояний | а, m а ; b, m b > с соответствующими коэффициентами — коэффициентами Клебша — Гордона для каждого отдельного члена. Можно считать, что эти коэффициенты дают «количест­во» состояния | j a , m a ; j b , m b >, проявляющегося в состоянии

Таблица 16.7 · ОБЪЕДИНЕНИЕ ДВУХ ЧАСТИЦ СО СПИНОМ 1 ( j a =1, j b =1)

I /, My. Так что каждый из коэффициентов Клебша — Гордона обладает, если угодно, шестью индексами, указывающими его положение в формулах типа приведенных в табл. 16.3 и 16.6. Иначе говоря, обозначая, скажем, эти коэффициенты С ( J , М; j a , m a ; j b , m b ), можно выразить равенство во второй строчке табл. 16.6 так:

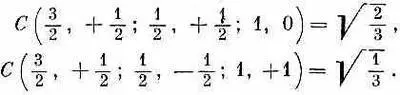
Мы не будем здесь подсчитывать коэффициенты для других частных случаев. Но вы обнаружите такие таблицы во мно­гих книжках. Попробуйте сами подсчитать другой случай, например объединение двух объектов со спином 1. Мы же про­сто привели в табл. 16.7 окончательный результат.

Эти законы объединения моментов количества движения имеют очень важное значение в физике частиц, их приложениям поистине нет конца. К сожалению, у нас нет сейчас больше вре­мени на другие примеры.

Добавление 1. Вывод матрицы поворота

Для тех, кто хотел бы разобраться в этом поподробнее, мы вычислим сейчас общую матрицу поворота для системы со спи­ном (полным моментом количества движения) j . В расчете об­щего случая на самом деле большой необходимости нет; важно понять идею, а все результаты вы сможете найти в таблицах, которые приводятся во многих книжках. Но, с другой стороны, вы зашли уже так далеко, что у вас, естественно, может возник­нуть желание убедиться, что вы и впрямь в состоянии понять даже столь сложные формулы квантовой механики, как (16.35).

Расширим рассуждения § 4 на систему со спином j , которую будем считать составленной из 2/ объектов со спином 1/ 2. Состоя­ние с m=j имело бы вид | + + + . . . +> (с j плюсами). Для m=j- 1 было бы 2 j членов типа | + + . . . + + ->, | + + . . . +- +>и т. д. Рассмотрим общий случай, когда имеет­ся r плюсов и s минусов, причем r + s =2 j . При повороте вокруг оси r от каждого из r плюсов появится множитель e + i j /2 . В итоге фаза изменится на i ( r /2- s /2)j. Мы видим, что

m=(r-s)/ 2 . (16.59)

Как и в случае J = 3/ 2, каждое состояние с определенным т должно быть суммой всех состояний с одними и теми же r и s, взятых со знаком плюс, т. е. состояний, отвечающих всевозмож­ным перестановкам с r плюсами и s минусами. Мы считаем, что вам известно, что всего таких сочетаний есть (r+s)!/r!s!. Чтобы нормировать каждое состояние, надо эту сумму разделить на корень квадратный из этого числа. Можно написать

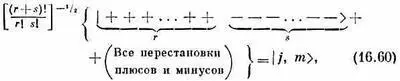
где

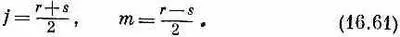
Введем еще новые обозначения, они нам помогут в счете. Ну а поскольку мы уж определили состояния при помощи (16.60), то два числа r и s определяют состояние ничуть не хуже, чем j и m. Мы легче проследим за выкладками, если обозначим

где [см.. (16.61)]

r = j+m, s = j-т.

Далее, (16.60) мы запишем, пользуясь специальным обозна­чением

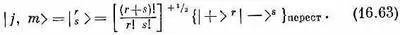
Обратите внимание, что показатель степени в общем множителе мы изменили на + 1/ 2. Это оттого, что внутри фигурных скобок в (16.60) стоит как раз N =(r+s)!/r!s! слагаемых. Если сопоста­вить (16.63) с (16.60), то ясно, что