Ричард Фейнман - 9. Квантовая механика II

§ 9. Переходы Джозефсона

И вот напоследок я перехожу к разбору очень интересного случая, впервые отмеченного Джозефсоном, к анализу того, что бывает при контакте двух сверхпроводников. Пусть у нас есть два сверхпроводника, связанные тонким слоем изолятора (фиг. 19.6).

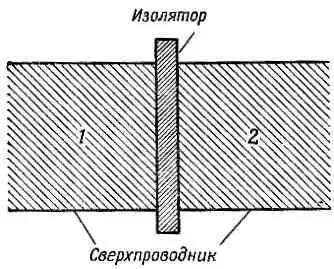
Фиг. 19.6. Два сверхпроводника, разделенных тонким изолятором.

Теперь такое устройство называется «переходом Джозефсона». Если изолирующий слой толст, электроны не могут пройти через него, но если он достаточно тонок, то элект­роны могут иметь заметную квантовомеханическую амплитуду перескока. Это попросту новый пример квантовомеханического проникновения через барьер. Джозефсон проанализировал та­кой случай и выяснил, что при этом должно происходить немало странных явлений.

Для анализа такого контакта я обозначу амплитуду того, что электрон окажется на одной стороне, через y 1, а того, что на другой,— через y 2. В сверхпроводящем состоянии волновая функция y 1— это общая волновая функция всех электронов с одной стороны, а y 2— соответствующая функция с другой стороны. Эту задачу можно решать для сверхпроводников раз­ного сорта, но мы ограничимся самым простым случаем, когда вещество по обе стороны одно и то же, — так что соединение са­мое простое и симметричное. И пусть пока никакого магнитного поля нет. Тогда связь между этими двумя амплитудами должна быть такой:

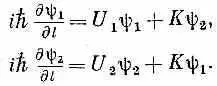
Постоянная К характеризует данный переход. Если бы К была равна нулю, то эта пара уравнений попросту описывала бы наинизшее энергетическое состояние (с энергией U) каж­дого сверхпроводника. Но обе стороны связаны амплитудой К, выражающей возможность утечки из одной стороны в другую (это как раз известная нам по двухуровневым системам ампли­туда «переброса»). Если обе стороны одинаковы, то U 1будет равно U 2, и я имею право их просто вычесть. Но теперь пред­положим, что мы подсоединили две сверхпроводящие области к двум полюсам батарейки, так что к переходу оказалась при­ложенной разность потенциалов V. Тогда U 1 -U 2 =qV. Для удобства я могу выбрать нуль энергии посредине между U 1и U 2, и тогда уравнения обратятся в

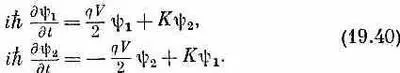
Это стандартные уравнения двух связанных квантовомеханических состояний. На этот раз давайте проанализируем их по-иному. Сделаем подстановки:

где q 1и q 2— фазы по обе стороны контакта, a r 1и r 2— плотно­сти электронов в этих двух точках. Вспомним, что на практике r 1и r 2почти точно совпадают друг с другом и равны r 0— нормальной плотности электронов в сверхпроводящем материале. Если вы теперь подставите эти формулы для y 1и y 2в (19.40) и приравняете вещественные части вещественным, а мни­мые — мнимым, то получится четверка уравнений (для крат­кости обозначено q 2-q 1=d):

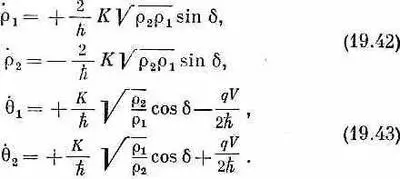
Первая пара уравнений говорит, что r 1=-r 2«Но,— ска­жете вы,— они ведь обе должны быть равны нулю, раз r 1и r 2обе постоянны и равны r 0». Не совсем. Эти уравнения описывают не все. Они говорят, какими были бы r 1и r 2, если бы не было до­бавочных электрических сил за счет того, что нет баланса между электронной жидкостью и фоном положительных ионов. Они сообщают, как начали бы меняться плотности, и поэтому описывают тот ток, который начал бы течь. Этот ток, текущий от стороны 1 к стороне 2, был бы как раз равен r 1(или -r 2), или

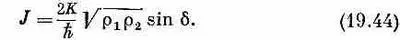
Такой ток вскоре зарядил бы сторону 2, если можно было бы за­быть, что обе стороны соединены проводами с батареей. Однако он не зарядит область 2 (и не разрядит область 1), потому что возникнут токи, которые выровняют потенциал. В наши урав­нения эти токи от батареи не входят. Если бы их добавить, то r 1и r 2оставались бы фактически постоянными, а ток через переход определялся бы формулой (19.44).

Поскольку r 1и r 2действительно остаются постоянными и равными r 0, давайте положим 2K r 0 /h=J 0 и напишем

J = J 0sind. (19.45)

Тогда J 0, подобно К, есть число, характеризующее данный переход.

Другая пара уравнений (19.43) дает нам q 1и q 2. Нас инте­ресует разность d=q 2-q 1, которую мы хотим подставить в (19.45); из уравнений же мы имеем

Это значит, что можно написать

где d 0— значение d при t= 0 . He забывайте также, что q — это заряд пары, q= 2 q e . В уравнениях (19.45) и (19.47) содер­жится важный результат — общая теория переходов Джозефсона.

Так что же из них следует? Сначала приложим постоянное напряжение. Если приложить постоянное напряжение V 0, то аргумент синуса примет вид d 0 +(q/h)V 0 t. Поскольку h/q— чис­ло маленькое (по сравнению с обычными напряжениями и вре­менами), то синус будет колебаться довольно быстро и в итоге никакой ток не пойдет. (Практически, поскольку температура не равна нулю, небольшой ток все же будет из-за проводимости «нормальных» электронов.) С другой стороны, если напряже­ние на переходе равно нулю, то ток может пойти! Если нет на­пряжения, то ток может равняться любой величине между + J 0и - J 0(в зависимости от того, каково значение d 0). Но попробуй­те приложить напряжение — и ток обратится в нуль. Это стран­ное поведение недавно наблюдалось экспериментально.

Ток можно получить и другим способом: кроме постоянного напряжения — приложить еще и высокую частоту. Пусть

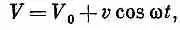
где v< Тогда

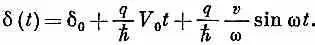
Но при малых D x

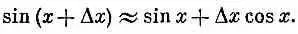
Разложив по этому правилу sind, я получу