Ричард Фейнман - 9. Квантовая механика II

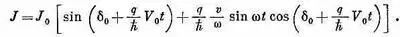
Первый член в среднем дает нуль, но второй в нуль не об­ращается, если

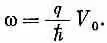
Значит, если частота переменного напряжения равна (q/h)V 0 , то через контакт пойдет ток. Шапиро сообщил, что он наб­людал такой резонансный эффект.

Если вы просмотрите работы на эту тему, то заметите, что в них формула для тока часто записывается в виде

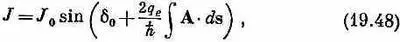
где интеграл берется по пути, ведущему через переход. Причина здесь в том, что если переход находится в поле векторного по­тенциала, то фаза амплитуды переброса видоизменяется так, как было объяснено вначале [уравнение (19.1)]. Если вы всюду включите такой сдвиг фазы, то получите нужные формулы.

Наконец, я хотел бы описать очень эффектный и интерес­ный опыт по интерференции токов, проходящих через два пере­хода, который был недавно проделан. Мы привыкли встречаться в квантовой механике с интерференцией амплитуд от двух ще­лей. Сейчас мы будем иметь дело с интерференцией двух токов, текущих через два перехода между сверхпроводниками. Она вызывается различием в фазах, с которыми сливаются токи, прошедшие по двум разным путям. На фиг. 19.7 показано па­раллельное соединение двух переходов а и b между сверхпровод­никами.

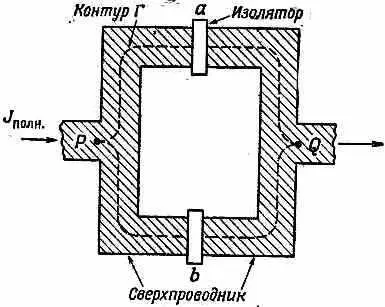
Фиг. 19.7. Два па­раллельных перехода Джозефсона.

Концы сверхпроводников Р и Q подключены к прибо­рам, которыми мы измеряем ток. Внешний ток J полнбудет суммой токов через каждый из переходов. Пусть J a и J b это то­ки через переходы, и пусть их фазы будут d а и d b . Разность фаз волновых функций в точках Р и Q должна быть одинаковой, по какому бы пути вы ни пошли. На том пути, который следует через переход а, разность фаз между Р и Q равна d а плюс кри­волинейный интеграл от векторного потенциала вдоль верхнего пути:

Почему? Потому что фаза q связана с Ауравнением (19.26). Если вы это уравнение проинтегрируете вдоль какого-то пути, то левая часть даст изменение фазы, которое тем самым как раз окажется пропорциональным криволинейному интегралу от А, что и написано. Изменение фазы по нижнему пути может быть записано подобным же образом:

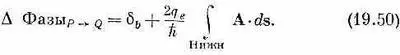
Эти величины должны быть равны; если я их вычту, то получу, что разность дельт должна быть равна контурному интегралу от Апо замкнутому пути

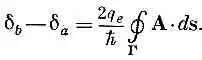
Здесь интеграл берется по замкнутому контуру Г (см. фиг. 19.7), проходящему через оба перехода. Интеграл от А это магнитный поток Ф через контур. Итак, две дельты оказываются отличаю­щимися на 2 q e /h, умноженное на магнитный поток Ф, который проходит между двумя ветвями схемы:

Изменяя магнитное поле в схеме, я смогу контролировать эту разность фаз. Я ее прилажу так, чтобы посмотреть, проявится ли в полном токе, текущем сквозь оба перехода, интерференция между его частями. Полный ток равен сумме J a и J b . Для удоб­ства я приму

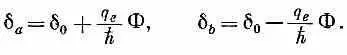
Тогда

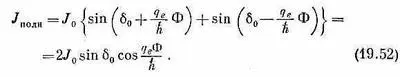
Мы не знаем, каково значение d 0, и природа здесь может, в зависимости от обстоятельств, вытворять все, что ей заблаго­рассудится. В частности, d 0может зависеть от прилагаемого к переходам внешнего напряжения. Но что бы мы ни делали, sind 0не окажется больше единицы. Значит, предельно сильный ток для каждого данного Ф дается формулой

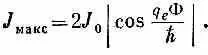
Этот предельный ток меняется, смотря по тому, каково Ф, и сам достигает максимума всякий раз, когда

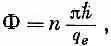
где n — целое число. Иными словами, ток достигает своего максимума, когда зацепляющийся за схему поток принимает те самые квантованные значения, которые мы получили в уравнении (19.30)!

Ток Джозефсона через двойной переход недавно был изме­рен как функция магнитного поля в области между ветвями. Результаты приведены на фиг. 19.8.

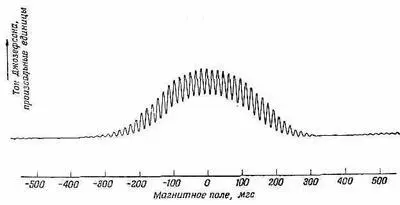
Фиг. 19.8. Запись тока через два параллельных перехода Джозефсона как функции магнитного поля в области между двумя переходами.

Здесь мы видим общий фон от токов, вызываемых различными эффектами, которыми мы пренебрегли, но быстрые колебания тока при изменении маг­нитного поля объясняются наличием интерференционного члена cos(q e Ф/h) в (19.52).

Один из самых интригующих вопросов квантовой механики— это вопрос о том, существует ли векторный потенциал в том месте, где нет поля. Опыт, который я только что описал, был проделан тоже с узеньким соленоидом, помещенным между дву­мя переходами, так что заметное магнитное поле В было только внутри соленоида, а на сверхпроводящие провода его попа­дало пренебрежимо мало. И вот оказалось, что сила тока колеблется с изменением потока магнитного поля внутри этого соленоида, даже если само поле и не касается проводов. Это еще одно доказательство «физической реальности» векторного по­тенциала [см. гл. 15, § 5 (вып. 6)].

Я не знаю, что теперь на очереди. Но посмотрите-ка, что можно было бы сделать. Во-первых, заметьте, что интерференция между двумя переходами может быть применена для создания чувствительного магнитометра. Если площадь, охватываемая двумя переходами, равна, скажем, 1 мм 2 , то максимумы на кри­вой фиг. 19.8 будут отстоять друг от друга на 2·10 -5 гс. Одну десятую промежутка между пиками запросто можно заметить; значит, таким соединением можно будет измерять поля вели­чиной в 2·10 -6 гс , или замерять большие поля со столь же хоро­шей точностью. Можно даже пойти дальше. Представим, на­пример, что мы вплотную друг к другу на равных расстояниях расставили 10—20 переходов. Тогда получится интерференция на 10—20 щелях, и при изменении магнитного поля мы полу­чим очень резкие максимумы и минимумы. Вместо интерфе­ренции на двух щелях у нас будет двадцати-, а может быть, и стощелевой интерферометр для измерения магнитного поля. Вероятно, можно предсказать, что измерения магнитных полей при использовании квантовомеханической интерференции ста­нут почти такими же точными, как измерения длин световых волн.