Ричард Фейнман - 6a. Электродинамика

Дифференцирование по времени даст нам просто еще один множитель iw:

(23.7)

Как и ожидалось, наведенное поле стремится свести на нет первоначальное электрическое поле. Исправленное поле Е = Е 1 +Е 2 тогда равно

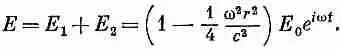
(23.8)

Электрическое поле в конденсаторе больше уже не однород­но; оно имеет параболическую форму (штриховая линия на фиг. 23.5). Вы видите, что наш простенький конденсатор уже слегка усложняется.

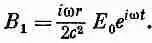
Наши результаты можно использовать для того, чтобы под­считать импеданс конденсатора на больших частотах. Зная электрическое поле, можно подсчитать заряд обкладок и узнать, как ток через конденсатор зависит от частоты оз. Но эта задача нас сейчас не интересует. Нас больше интересует другое: что станется, если частота будет продолжать повышаться, что про­изойдет на еще больших частотах? Но разве мы уже не кончили наш расчет? Нет, потому что раз мы исправили электрическое поле, то, значит, магнитное поле, которое мы раньше подсчи­тали, больше уже не годится. Приближенно магнитное поле (23.5) правильно, но только в первом приближении. Обозначим его В 1, а (23.5) перепишем в виде

(23.9)

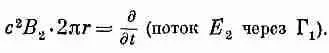
Вспомните, что это поле появилось от изменения Е 1. А правиль­ное магнитное поле будет создаваться изменением суммарного электрического поля Е 1+Е 2. Если магнитное поле представить в виде В=В 1+В 2 , то второе слагаемое — это просто добавочное поле, создаваемое полем Е г .Чтобы узнать В 2, надо повторить все те же рассуждения, которые приводились, когда подсчиты­вали В 1: контурный интеграл от B 2вдоль кривой Г 1равен ско­рости изменения потока Е 2через Г 1. Опять получится то же уравнение (23.4), но В в нем надо заменить на В 2, а Е — на E 2:

Поскольку Е 2 с радиусом меняется, то для получения его пото­ка надо интегрировать по круговой поверхности внутри Г 1. Беря в качестве элемента площади 2prdr, напишем этот интеграл в виде

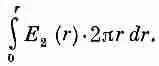
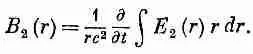
Значит, В 2 (r) выразится так:

(23.10)

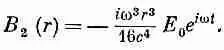
Подставляя сюда Е 2 (r) из (23.7), получаем интеграл от r 3 dr, который равен, очевидно, r 4 /4. Наша поправка к магнитному полю окажется равной

(23.11)

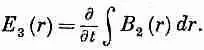
Но мы еще не кончили! Раз магнитное поле В вовсе не такое, как мы сперва думали, то мы, значит, неверно подсчитывали Е 2. Надо найти еще поправку к Е, вызываемую добавочным магнит­ным полем В 2. Эту добавочную поправку к электрическому по­лю назовем Е 3. Она связана с магнитным полем В 2так же, как E 2была связана с В 1. Можно опять прибегнуть к тому же самому соотношению (23.6), изменив в нем только индексы:

(23.12)

Подставляя сюда наш новый результат (23.11), получаем новую поправку к электрическому полю:

(23.13)

Если теперь наше дважды исправленное поле записать в виде Е=Е 1 +Е 2 +Е 3 , то мы получим

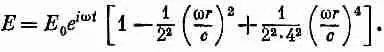
(23.14)

Изменение электрического поля с радиусом происходит уже не по параболе, как было на фиг. 23.5; на больших радиусах значе­ние поля лежит чуть выше кривой (E 1+E 2).

Мы пока еще не дошли до конца. Новое электрическое поле вызовет новую поправку к магнитному полю, а заново под­правленное магнитное поле вызовет необходимость дальнейшей поправки к электрическому и т. д. и т. д. Но у нас уже есть все нужные формулы. Для В 3 можно использовать (23.10), изменив индексы при В и Е с 2 до 3.

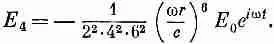
Очередная поправка к электрическому полю равна

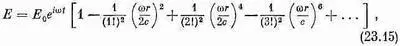
С этой степенью точности все электрическое поле дается, стало быть, формулой

где численные коэффициенты написаны в таком виде, что стано­вится ясно, как продолжить ряд.

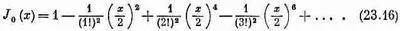
Окончательно получается, что электрическое поле между обкладками конденсатора на любой частоте дается произведением E 0e i w tна бесконечный ряд, который содержит только перемен­ную wr/с. Можно, если мы захотим, определить специальную функцию, обозначив ее через J 0(x), как бесконечный ряд в скоб­ках формулы (23.15):

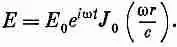
Тогда искомое решение есть произведение E 0 e i w t на эту функцию при x=wr/c:

(23.17)

Мы обозначили нашу специальную функцию через J 0 по­тому, что, естественно, не мы первые с вами занялись задачей колебаний в цилиндре. Функция эта появилась давным-давно, и ее уже привыкли обозначать J 0 . Она всегда возникает, когда вы решаете задачу о волнах, обладающих цилиндрической сим­метрией. Функция J 0 по отношению к цилиндрическим волнам — это то же, что косинус по отношению к прямолинейным волнам. Итак, это очень важная функция. И изобретена она очень давно. Затем с нею связал свое имя математик Бессель. Индекс нуль означает, что Бессель изобрел целую кучу разных функций, а наша — самая первая из них.

Другие функции Бесселя — J 1?J 2и т. д.— относятся к цилиндрическим волнам, сила которых меняется при обходе вокруг оси цилиндра.

Полностью скорректированное электрическое поле между обкладками нашего кругового конденсатора, даваемое формулой (23.17), изображено на фиг. 23.5 сплошной линией. Для не очень больших частот нашего второго приближения вполне хватает. Третье приближение было бы еще лучше — настолько хорошо, что если его начертить, то вы бы не заметили разницы между ним и сплошной линией. В следующем параграфе вы уви­дите, однако, что может понадобиться и весь ряд, чтобы получи­лось аккуратное описание поля на больших радиусах или на больших частотах.