Александр Филиппов - Многоликий солитон

Как вы помните, уравнение Д'Аламбера не зависело от знака v 0и описывало волны, бегущие в обоих направлениях. Уравнение для дислокаций также обладало этим свойством. Почему же КдФ-уравнение не обладает этим свойством, в то время как волны на поверхности ручья от брошенного камня бегут в обоих направлениях *)?

*) Кортевег и де Фриз вывели свое уравнение из уравнения Буссинеска, которое больше похоже на уравнение Д'Аламбера и описывает волны, бегущие в обоих направлениях. Уравнение Буссинеска, однако, сложнее, чем КдФ-уравнение.

Ответ на этот вопрос на самом деле очень простой. Если нас не интересует начальный момент, когда от брошенного в ручей камня начинают разбегаться две волны, то мы можем отдельно изучать одну и другую. Если эффекты нелинейности и дисперсии достаточно малы, то обе волны убегут на большое расстояние друг от друга за столь малое время, что эти эффекты не успеют сказаться, и в дальнейшем можно следить за судьбой одной из волн, забыв о существовании другой. Именно поэтому можно описывать эволюцию обеих волн одинаковым по виду уравнением с разными знаками перед v 0. (В случае дислокаций, когда эффекты нелинейности и дисперсии всегда велики, так поступить нельзя!)

Эта идея, в сущности очень простая, привела к огромному упрощению, которое позволило Кортевегy и де Фризу правильно понять природу солитона Рассела, а спустя 70 лет привело к созданию полной математической теории солитонов. С точки зрения физиков, теория солитонов на основе КдФ-уравнения кажется наиболее понятной, так как в ней наглядно видно, каким образом уравновешивание эффектов нелинейности и дисперсии приводит к образованию устойчивой уединенной волны. Мы больше не будем касаться математики солитонов, она достаточно сложна, а посмотрим на устройство солитона глазами физика.

Итак, если нет ни дисперсии, ни нелинейности, по поверхности могут распространяться импульсы любой формы, но это не солитоны. Всегда имеющиеся в физической системе малые эффекты дисперсии и трения вскоре исказят первоначальный импульс до неузнаваемости. Посмотрим, как влияет на него нелинейность. Заметим, что КдФ-уравнение с выброшенным последним членом, ответственным за дисперсию, можно решить точно. Метод решения был известен еще Лагранжу, однако его первые применения к реальным нелинейным волнам связаны с именем знаменитого немецкого математика Георга Фридриха Бернхарда Римана (1826—1866).

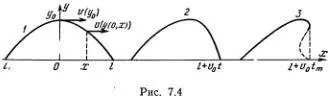
Пусть на поверхности воды образовался горбик, изображенный на рис. 7.4, кривая 1 . Дальнейшая судьба этого горбика определяется тем, что скорость каждой точки графика зависит от ее высоты.

Для волн КдФ эта зависимость простейшая:

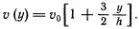
Быстрее всех движется вершина горбика. Ее скорость равна

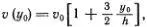
а скорость переднего фронта горбика, где у = 0, равна v 0. Поэтому в некоторый следующий момент времени передняя часть горбика станет более крутой (кривая 2), а с течением времени произойдет «опрокидывание» волны (кривая 3), которое уже нельзя описать на этом простом языке. Такое опрокидывание волн все мы много раз видели, когда наблюдали прибой на берегу моря или на речной отмели.

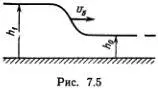
Не так легко, и притом небезопасно, наблюдать другое явление, вызванное описанным увеличением крутизны фронта волны. Если приливная волна из моря входит в устье реки, то может образоваться волна в виде высокой, крутой ступеньки (рис. 7.5), которую называют бором .

Бор — один из примеров ударной волны . Хорошо знакомый нам пример ударной волны — взрывной звук, который слышен, когда реактивный самолет проходит звуковой барьер. Более идиллический пример — щелчок пастушьего кнута.

Ударные волны были открыты Риманом в 1860 г. Он, однако, сомневался в возможности их наблюдения, в то время как Рассел уже заметил, что скорость распространения звука от пушечного выстрела больше, чем обычно измеряемая скорость звука в воздухе («звук пушечного выстрела доносится быстрее, чем команда открыть огонь»). Здесь Рассел действительно подметил одно из важных свойств ударной волны. Например, скорость движения бора равна v Б= 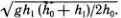Так как h 1 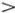h 0, то 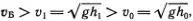и бор бежит быстрее, чем любая небольшая волна на поверхности воды с глубинами h 0или h 1. Увеличение крутизны фронта волны и ее опрокидывание превращает гигантский, но безвредный океанский солитон в страшное стихийное бедствие — цунами.

Ударная волна в воздухе — очень сложное явление. На фронте ударной волны резким скачком возрастают давление, температура и плотность. Однако плотность не увеличивается выше определенного предела, тогда как давление и температура могут быть огромными. Например, при скачке давления в 100 атмосфер температура фронта волны достигает 3500 градусов. При такой температуре в молекулах возбуждаются сильные внутренние колебания и часть молекул кислорода даже распадается на атомы, возникают химические реакции. При более высокой температуре возникает очень сильное свечение. Апокалиптическое явление ударной волны (огненный шар «ярче тысячи солнц») печально известно из описаний ядерного взрыва, когда температура выше 10 000 градусов, а давление достигает 1000 атмосфер. Не дай нам Бог увидеть эту ударную волну!

Колоссальная ударная волна образовалась при падении знаменитого тунгусского метеорита (30 июня 1908 г.)*). Перед его падением в течение нескольких секунд был виден ослепительно яркий огненный шар, в момент падения раздался оглушительный взрыв, который слышали на расстоянии больше тысячи километров. Воздушная взрывная волна была зарегистрирована даже в Англии! По современным оценкам примерно такую волну вызывает ядерный взрыв в несколько Мегатонн. Однако тунгусская ударная волна не была вызвана ядерным взрывом. Она того же происхождения, что и ударные волны, возникающие при переходе самолетом «звукового барьера». Иными словами, она была вызвана движением небесного тела в атмосфере со сверхзвуковой скоростью. Может быть, это была комета или ее кусок.