С. Егоров - Коллоидная химия. Шпаргалка

Величина поверхностного натяжения является постоянной величиной при постоянной температуре, она характеризует полярностьжидкости, или интенсивностьполя молекулярных сил.

Эта характеристика молекулярного сцепления связана с такими параметрами, как дипольный момент, поляризуемость, диэлектрическая проницаемость. Полярность растет с увеличением значений дипольного момента и диэлектрической проницаемости.

Существуют и другие компоненты молекулярных сил, проявляющиеся, например, у молекул с двойными связями.

Для границы двух несмешивающихся жидкостей всегда необходимо учитывать межмолекулярное сцепление соседней фазы.

Действие межмолекулярных сцеплений, как правило, представляется аддитивным, поэтому значение поверхностного натяжения для границы двух жидкостей определяется разностью их интенсивностей.

Само поверхностное натяжение называют в данном случае пограничным(или межфазным) поверхностным натяжением. Существование аддитивности действия молекулярных сил выражается правилом Антонова, которое гласит, что пограничное натяжение σ жж равно разности поверхностных натяжений этих жидкостей (на границах с воздухом) в условиях взаимного насыщения. Математически данное правило можно записать следующим образом:

σ жж = σ жг 1– σ жг 2 ,

где s жж – межфазное поверхностное натяжение на границе «жидкость – жидкость»;

σ жг 1, σ жг 2 – значения поверхностных натяжений этих жидкостей на границе с воздухом.

Поясним правило Антонована примере смеси двух жидкостей – воды и бензола.

Пусть слагаемое σ жг 1 относится к насыщенному раствору бензола в воде, а слагаемое σ жг 2 – к насыщенному раствору воды в бензоле.

С уменьшением разностей полярностей увеличивается взаимная растворимость жидкостей, различие между свойствами сосуществующих постепенно исчезает, а значения σ жг 1 и σ жг 2 становятся более близкими.

Следовательно, значение межфазного поверхностного натяжения σ жж уменьшается. В том случае, когда происходит полное взаимное растворение, значение межфазного поверхностного натяжения становится равным нулю.

Если представить, что данную смесь возможно разделить на два искомых вещества, то для этого необходимо совершить работу, направленную на разрыв межфазной поверхности и образование двух новых межфазных поверхностей.

Эта работа называется работой адгезии. Математически ее можно записать следующим образом:

W = σ жг 1+ σ жг 2– σ жж.

На границе твердого тела с жидкостью или газом также существует избыточное поверхностное натяжение.

Однако его сложно характеризовать как межфазное, поскольку процессы образования новой поверхности необратимы.

Значения избыточного поверхностного натяжения на границах «твердое тело – жидкость» или «твердое тело – газ» намного превышают аналогичные величины на межфазных поверхностях «жидкость – жидкость» или «жидкость – газ», поскольку интенсивность силового поля в твердых телах больше, чем в жидких состояниях вещества.

Поверхность раздела фаз на практике довольно часто оказывается не плоской, а искривленной. Поверхность раздела фаз может быть выпуклой или вогнутой. Молекула жидкости, находящаяся на выпуклой поверхности, будет испытывать равнодействующую силу, меньшую, чем на плоской поверхности и направленную в глубь жидкости.

На вогнутой поверхностиэта сила больше. Вследствие изменения поверхностных взаимодействий происходит изменение условий равновесия фаз, разделенных искривленной поверхностью.

На искривленной поверхности, помимо общего давления в обеих сосуществующих фазах, возникает добавочное давление, направленное в сторону той фазы, по отношению к которой поверхность вогнута, т. е. давление в фазе, отделенной от другой фазы вогнутой поверхностью, больше. Разность давлений, возникающая по обе стороны искривленной поверхности жидкости, получила название капиллярного давления, иначе его называют лапласовым давлением.

Величина капиллярного давления зависит от кривизны поверхности и поверхностного натяжения и выражается уравнением Лапласа. Рассмотрим вывод данного уравнения. Пусть нам дан элементарный участок искривленной поверхности площадью

s = L 1 L 2,

где L 1 и L 2 – криволинейные отрезки, ограничивающие искомый участок.

Радиусы кривизны криволинейных отрезков равны r 1 , r 2 , следовательно, площадь s равна:

s = L 1 L 2= r 1 φ 1… r 2 φ 2,

где φ 1 и φ 2 – соответствующие центральные углы.

Если под действием силы, вызванной разностью давлений Δр по обе стороны поверхности, произошло смещение поверхности на величину dr без изменения кривизны, то имеет место увеличение этой поверхности на величину ds.

Затраченная работа dW может быть вычислена как произведение силы на путь или как произведение поверхностного натяжения на прирост поверхности следовательно,

dW = σds = Δ рsdr = r 1 r 2 φ 1 φ 2 Δрdr.

Таким образом, величина ds будет определена как

ds = (r 1+ dr) x (r 2+ dr)φ 1 φ 2– r 1r 2 φ 1 φ 2.

Преобразовав данное уравнение, пренебрегая бесконечно малыми величинами, получим:

ds = φ 1 φ 2r 1 dr – φ 1 φ 2 r 2 dr.

Пользуясь полученными уравнениями, получим уравнение Лапласа, выражающее избыток давления со стороны вогнутой поверхности:

Δр = σ(r 1 –1+ r 2 — 1).

Если поверхность сферическая, то r 1= r 2, а уравнение Лапласа примет вид:

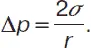
Величина давления насыщенного пара жидкости при данной температуре зависит от формы поверхности. Капиллярные явления– это явления физического свойства. Действие поверхностного натяжения происходит на границе раздела несмешивающихся сред. К капиллярным явлениям относят явления в жидких средах, вызванные искривлением их поверхности, граничащей с состояниями сред. Искривление поверхности ведет к появлению в жидкости дополнительного капиллярного давления, оно обозначается Δp, величина которого связана со средней кривизной r поверхности уравнением Лапласа.

В пористых телах наряду с адсорбцией часто имеет место явление капиллярной конденсации. Под капиллярной конденсацией понимают конденсацию пара адсорбата при давлениях, которые меньше давления насыщенного пара. При адсорбции происходит образование тонкой пленки адсорбированного вещества на стенках пор, которые довольно хорошо смачиваются жидким сорбатом, в результате чего имеет место образование вогнутого мениска жидкости. Согласно закону Томсона давление пара, равновесное вогнутой поверхности, меньше упругости насыщенного пара. Следовательно, конденсация пара в порах над вогнутым мениском начинается при давлениях, которые меньше давления насыщенного пара. Изотерма адсорбции в случае капиллярной классификации принадлежит к одному из типов 2–5 по классификации Брунаура.