Н. Болотов - Параллельные

С другой стороны, если мы принимаем безразмерный амер за единицу и структуру пространства, то это самое пространство резонно измерять в амерах, которые могут, видимо, быть и ничтожно малыми и бесконечно большими. Оттого переходная зона может иметь любые размеры, в том числе и Вселенские.

В этом плане меня всегда удивлял парадокс неэвклидовых геометрий, утверждающий, что кривизна пространства возрастает с увеличением его размеров, читай – радиуса. В тоже время соприкасание евклидова и неэвклидова пространств (по этой же теории) возможно при уменьшении «тензора кривизны», то есть кривизны окружности при увеличении её радиуса. Такой нелепости эвклидова геометрия не допускает (смотрите рисунок).

Окружность при бесконечном увеличении радиуса трансформируется в бесконечную линию.

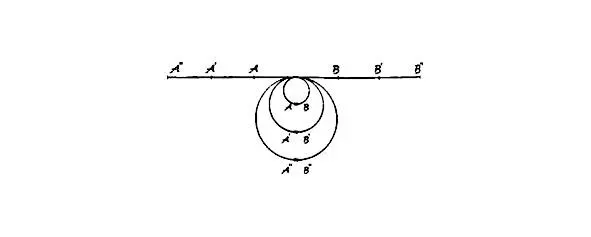
Вот такой парадокс!

Но, а если совсем уж просто, то этот рисунок показывает и путь достижения бесконечно далекой цели. Для этого не обязательно долго, долго двигаться от точки А ″ через А′, А до В, В′,В″, следует повернуть назад (см. как они фактически замыкаются на окружностях) и ты уже дома. И не только в этом столетии, по летоисчислению теории относительности, а уже просто напросто завтра, а и того лучше – мгновенно…

Крус, сам не ожидая от себя такой залихватости, почесал затылок.

– Я не уверен, что приведенный мною примитив имеет какое-либо фундаментальное значение, но в плане точки отчета и как вариант для проектирования эксперимента принять схему можно.

Авкуб, довольно улыбнувшись рефрену в выступлениях физика и математика, заключил.

– Ну, да ладно, давайте, исходя из предложенных «примитивных» вариантов для проектирования эксперимента, подведем итоги…

Что мы имеем?

Во-первых, мы установили, что все происшедшее не плод «ушибленного» воображения Вана, которое вполне могло возникнуть при падении с высокого операторского кресла.

Во-вторых, самодеятельность Колотура, не самотключившегося (как ему было положено по инструкции) при попытке внешнего воздействия на программу, позволило нам, если не убедиться в существовании параллельного мира, то как – то его себе вообразить.

В-третьих, мы уже кое-что конкретно себе воображаем о конфигурации нашего и смежного пространства.

Вспомните синтез контура первичных «умозаключений» Колотура, посмотрите на его рисунок. Красный и зеленый человечки стоят на соответственно окрашенных сферах – плоскостях. Вероятно, мы имеем намек на возможные проявления эффектов гравитации и антигравитации в смежном пространстве, что Колотур представил нам в альтернативных цветах солнечного спектра – красным и зеленым.

В-четвертых, мы, вполне вероятно, наблюдали картину возможного материального перехода (депортации живого существа) между смежными мирами.

И наконец, в-пятых, «Снежный» своим, мягко говоря, не ординарным поведением предостерег своих сограждан, и попутно нас с вами, от чего-то смертельно опасного. Обратите внимание на (как мне представляется) «аннигиляционную вспышку» Колотуровской голограммы при пресечении (переходе) двух альтернативных (по каким—то признаком) пространств друг в друга, через нуль пространства.

И чтобы всем было понятно, что я имею в виду, посмотрите на эту голограмму, которую Колотур выдал в пояснение своим прежним аллегориям,

– Авкуб надел шлем сенсора и в воздухе появилась следующая фигура.

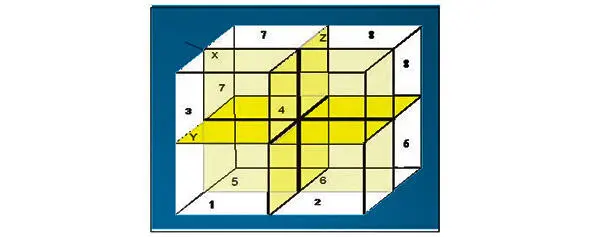
– То, что только «кажется» нашему математику, Колотур, без всякого сомнения постулирует, – продолжал шеф…

– Если поверхность сферы в бесконечности превращается в плоскость, то бесконечное сферическое пространство должно представлять собой безмерный куб, с чем я не могу не согласиться. Это бесконечное пространство Колотур разбивает, исходя из прямоугольной системы координат, условно, на восемь кубов.

С его точки зрения для этого достаточно трех обычных, пересекающихся в одной точке осей. Никакой четвертой оси «времени» для этого не требуется.

Посмотрите!

Каждый из кубов имеет (по смежным плоскостям) по три смежных пространства.

Может быть, переход через одно из них мы и наблюдали. Кроме того, вероятно, возможны какие-то перемещения и по смежным внутренним граням. Их у каждого куба также по три. Заметьте, что в этих случаях переходы осуществляются или по плоскости (двух мерному пространству), или по линии (одномерному пространству) и, видимо, нет «радикального» перехода только через точку нулевого пространства, через точку, на которую проецируется вся наша Вселенная

Это тоже логично, если мыслить «железной логикой колотуровской безмерности» – ведь точка в этом случае есть ноль!

А таких, предположительно «смертельных» для депортации материи из любой массы переходов по четыре пары (1—8, 2—7, 3—6 и 4—5). Это единственный случай четырехмерности у Колотура.

Другими словами, по Колотуру, депортация возможна в трёхмерном измерении (для пространств различной геометрии) и невозможна в четырехмерном, что вполне вероятно связано не с конфигурацией пространства, а с течением времени или с чем-то ещё. Видимо полная депортация возможна только при плоскостном переходе и частично в линейном.

В этом случае депортируется только «дух» материи, а именно, её торсионное биополе.

Остается надеяться, что мы наблюдали не линейный контакт…

В лаборатории наступила задумчивая тишина и в воздухе повис общий вопрос:

– Что будем делать?…

– А мы все вместе будем делать НИЧЕГО, – парировал всеобщее недоумение Авкуб.

– Кто из вас может интерпретировать формулу пространственного перехода Колотура в физическом эксперименте, даже использовав его заявку на патент?

Есть желающие?… Так, желающих нет!

Поэтому, по принципу «мы посоветовались и Я решил», принимаем такое постановление: каждый из вас (профессионалов) предлагает план эксперимента по форме передачи символов связи с той стороной, которые были бы понятны «параллельным» и вызывали бы у них интерес.

Всё остальное перепоручаем Колотуру без всякой цензуры с нашей стороны. Надеюсь, что автомат нас не подведёт и сможет «сдвинуть», хоть на миг, на наши «подарки» пространство параллельного мира…

Сергейчину предлагаю «накачать» самоанализ автомата до такой степени, чтобы он и помыслить не мог, что мы его «используем».

После загрузки «посыла» всем и каждому в отдельности следить за элементами и и этапами осуществления эксперимента. Особенно за представленными вами лично. Фиксировать любые мелочи. Никаких дополнительных поправок в первоначальный эксперимент не вносить и результатами не обмениваться.