Сергей Капица - Парадоксы роста. Законы глобального развития человечества

То же относится к культивированию системы ценностей, когда можно предвидеть более активное вмешательство как гражданского общества, так и государства в стихию хаоса и частные интересы, доминирующие в массмедийной системе. Для России архиважно сохранение традиций и развитие наших позиций в системе образования, показавшей свою состоятельность в эпоху перемен. Ведь суть образования состоит в понимании, а не в накоплении знаний, тем более что они все быстрее обесцениваются.

При этом науке и культуре все в большей степени переходит роль политических факторов, выражающих диктат демографического императива в глобальном развитии человечества. Значимым фактором является геополитическое пространство, где для России естественной ареной служит Евразийский суперконтинент. При сохранении давних связей с Европой для нас с учетом растущего значения потенциала и традиций Китая и Индии восточное направление становится приоритетным вектором развития: недаром наш герб увенчан двуглавым орлом.

Однако мерой нашего влияния и могущества должны стать культура и наука. С этим связаны надежды России и появляются основания для исторического оптимизма по выходу из кризиса, вызванного эпохой глобальной демографической революции, в которую нам довелось жить. Ибо «Блажен, кто посетил сей мир в его минуты роковые!»

История человечества подобна судьбе человека, который, пережив бурную молодость, время приключений и поисков, учился, воевал, обогащался и, наконец, женится, обретает семью и покой. Эта тема в мировой литературе существует со времен Гомера и сказок «Тысячи и одной ночи», писания св. Августина, Стендаля и Толстого: как и в живой природе, развитие особи повторяет эволюцию вида.

Только будущее это покажет, и ждать его не придется долго.

Быть может, теперь и человечеству после драматических времен роста и перемен предстоит одуматься и успокоиться.

Население мира N ( T ) будет описываться функцией от времени T , определяющей состояние демографической системы Земли. Тогда параметром порядка – ведущей переменной, подчиняющей все остальные переменные, – станет полное число людей N .

Таким образом, в этом приближенном функциональном соотношении не учитывается ни распределение населения по нашей планете, ни его экономическое и возрастное состояние или расовый и национальный состав. Сам процесс роста также будет рассматриваться на значительном интервале времени T – большом числе поколений. Иными словами, мы будем рассматривать усредненные значения переменных и усредненные функции. Этим, в частности, вносится в уравнения память о прошлом, определяемая временем усреднения переменных.

Такое выделение главных переменных N и T и их усреднение характерно для системного подхода. Оно получило развитие в синергетике и лежит в основе асимптотических методов, разработанных для решения задач большой сложности, появляющихся при рассмотрении систем со многими степенями свободы. Существенно то, что эти переменные, которые представляют все социально значимые факторы о возрасте и поле, образованию и развитию, доходам и т. д., описываются статистическими распределениями. Поэтому, когда рассматриваются такие многофакторные проблемы, то можно полагать, что в известных пределах развитие системы статистически стационарно и потому происходит динамически самоподобно. Это сильное предположение означает, что остаются неизменными пропорции между относительными изменениями времени и населения.

Смысл этой основной гипотезы автомодельности состоит в том, что утверждается постоянство относительной скорости изменения системы аналогично принципу инерции. В данном случае можно показать, что такой самоподобный рост должен описываться степенной функцией без характерного параметра, такого как масштаб времени. Такие процессы обладают масштабной инвариантностью – скейлингом – аналогично развитой турбулентности в потоке жидкости. Эти понятия мало знакомы историкам и обществоведам, однако они должны помочь в расширении тех образов, которыми мы описываем исторический процесс.

В книге показано, как данные демографии мира приводят к формуле (1):

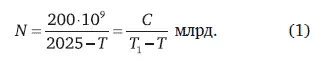
При обращении к формуле (1) задача теории в первую очередь состоит в установлении пределов ее применимости как вблизи особенности, когда эта функция устремляется в бесконечность, так и в далеком прошлом, когда ее уменьшение происходит слишком медленно. Иными словами, асимптотика ограничена в прошлом нулем и полюсом в настоящее время.

Чтобы описать переход, следует учесть время, характеризующее внутренние процессы, определяемое продолжительностью жизни человека и его репродуктивной деятельности – теми факторами, которые при прохождении через демографический переход ограничивают скорость роста по мере приближения к моменту, когда скорость роста приближается к своему пределу. Для этого следует обратиться к выражению для скорости роста в зависимости от времени, продифференцировав (1):

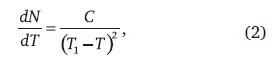
и затем ввести в это расходящееся выражение характерное время, ограничивающее скорость роста:

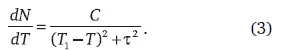
Этот прием может показаться произвольным шагом. Однако здесь мы обратились к методам, которые развиты для регуляризации расходимостей, появившихся в сингулярности роста. Полученное выражение очень хорошо описывает сингулярность глобального демографического перехода, поэтому, интегрируя (3), получим выражение для описания самого перехода и имеющего степенную асимптотику:

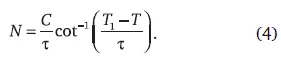
При обращении к последним данным демографии (см. рис. 18) были получены уточненные значения постоянных, что учтено во всех вычислениях:

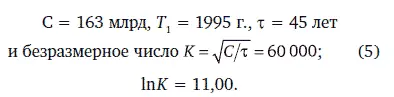
Из-за введения конечного τ полюс в Т 1сдвигается к новому значению Т 1= 1995 г., которое и принято при расчетах, описывающих как демографический переход, так и рост населения мира за пределы Т 1в выражении (4) (см. табл. 1).

В недалеком прошлом выражение (4) асимптотически непосредственно переходит в автомодельный гиперболический рост (1). Однако применительно к очень далекому прошлому скорость роста должна быть ограничена снизу. Этого предположения достаточно для того, чтобы приписать далекому прошлому линейный рост, при котором в первом приближении скорость роста не может быть меньше появления одного гоминида за время τ , пока численность населения не достигает ~100 000. В популяционной генетике число K характерно для численности стабильного вида, биологически подобного человеку. При достижении этого уровня в численности вида ~ 1,6 млн лет назад начинается эпоха квадратичного роста, которая становится доминирующей до момента демографического перехода.