Сергей Капица - Парадоксы роста. Законы глобального развития человечества

Из (15) следует, что после каждого цикла до демографического перехода остается половина времени длительности цикла:

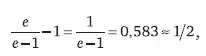
что вполне подтверждается данными истории и антропологии (см. табл. 2).

Рост населения можно иллюстрировать геометрическим построением функции тангенса:

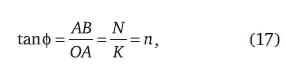
где угол ∆ φ = τ отображает течение времени, а приращение населения ∆ N = 1 и N 0= 1 (см. рис. 19).

Линейный рост будет продолжаться до φ A,B = Kτ = 1 и N B = tanl в точке В на касательной АС. Дальнейший рост N = K (π/2 – φ )–1 будет проходить по гиперболе, при которой время асимптотически стремится к π/2, а население достигнет значения N С = pK 2/2. Когда система приближается к моменту особенности, то от уравнения (16а) следует переходить к уравнению (16d), чтобы описать рост при прохождении особенности в течение эпохи С.

Построение на рис. 19 показывает, что после перехода от линейного к гиперболическому росту на эпоху Востается в два раза меньше времени, чем в начальную эпоху А. Для всей эпохи Ввремя от T 0до T 1при K = 7 разделено на 11 интервалов. Поскольку π/2 ≈ 11/7, то N C = K 2=49 в момент обострения. Однако даже при таком малом значении K , когда ln 7 = 1,95 дает хорошую оценку l + ln K ≈ 3 для числа демографических циклов.

Таким образом, нулевой цикл Аантропогенеза продолжался 7 единиц времени, первый цикл длился 3 и последний – 1 единицу времени. Это построение показывает, как дискретность времени и населения приводит к появлению периодичности роста, выраженной в демографических циклах.

Линейный рост описывает развитие системы от начальной сингулярности роста при N 0= 1 и положительных значений N . Далее следует рост по гиперболе и в конце – cингулярность демографического взрыва. Построение, когда переменные n и t при прохождении перехода меняются местами, мы оставляем читателю.

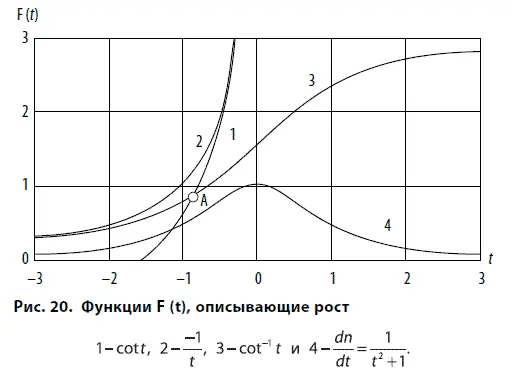
На рис. 20 показаны функции, описывающие рост системы при K = 1, которые появляются при построении решения, начинающегося с сингулярности в эпоху А,переходящего затем в эпоху Вгиперболического роста и завершающегося эпохой С. Асимптотический переход решений, описывающий рост в начале развития и на его конечном участке, получим, обратившись к рядам для функции cot–1( t/K ) и cot( t/K ):

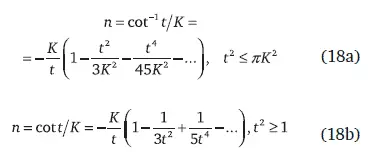
Эти функции пересекаются в точке А, посередине роста при логарифмическом представлении между временем Т 0 и Т 1, соответствующей наступлению неолита:

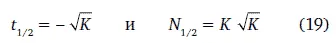
под углом 2/(3 K ) и практически гладко при K >>1.

Очевидно, что решение можно строить, отсчитывая время от T 0– от эпохи антропогенеза Aпри t 0= 0. Тогда, исключив t из (16c), получим одно автономное дифференциальное уравнение, описывающее рост в зависимости oт состояния системы, которое определяется населением Земли:

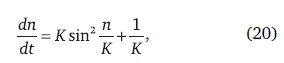
где последний член добавлен с тем, чтобы рост в эпоху Аникогда не был меньше одного гоминида при ∆ τ = τ .

Интегрируя (20) и при значениях K > 1 и начальных условиях t 0= n 0= 0, получим решение:

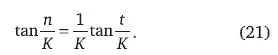
Это решение показывает симметрию переменных N и T – населения и времени. Для развития в течение эпохи Ввдали от особенностей роста это выражено в (16в) и следует из сложности причинных связей в рамках развитых представлений о нелинейной динамике глобальной системы населения нашей планеты.

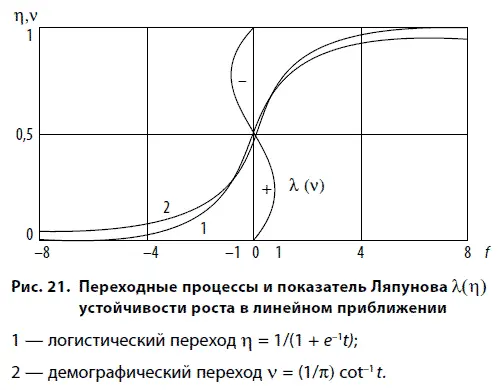
Для того чтобы выяснить устойчивость развития, следует обратиться к уравнению роста человечества (20). На основании (15) в линейном приближении устойчивость роста к возмущениям определяется показателем Ляпунова λ развития неустойчивости в системе населения (рис. 21):

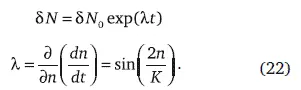
По этому критерию при λ > 0 движение до перехода неустойчиво и только после перехода развитие системы становится асимптотически устойчивым и впредь таким и остается. Более полное определение устойчивости потребует введения распределений для N и обращения к методам статистической физики при обобщении модели.

При гиперболическом росте мгновенное значение экспоненциального роста равно древности:

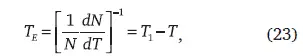
что и определяет скорость процессов развития в момент времени T .

В гиперболической хронологии мгновенный экспоненциальный масштаб времени роста и линейной неустойчивости по Ляпунову зависит от древности. До демографического перехода мгновенное значение времени равно удвоенному времени роста неустойчивости:

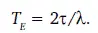
В глобальной системе населения мира можно предположить, что распределение населения городов и сел описывается степенным законом, имеющим фрактальную природу [52]. В таком случае это распределение хорошо описывается выражением:

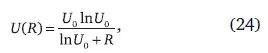
где R – ранг города, начиная с R = 0, а множитель ln U 0введен для подавления расходимости при R = 0. Тогда население самого крупного города U 0определяется решением трансцендентного уравнения, связывающего население мира N c U 0:

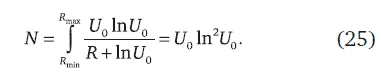
Обратимся к примерам: так, население Древнего Рима, где Колизей вмещал 50 000 зрителей, оказывается равным 1 млн при населении мира N =100 млн, что согласуется с оценками историков. С другой стороны, население Пекина в конце XVII в. достигало 3 млн при расчетном населении мира, равном 700 млн и оценках демографов в 900 млн. В 1985 г. при населении мира 4,8 млрд население Токио, как самого крупного города, было равно 17 млн (рис. 22). В 2011 г. при населении мира 7 млрд и население Токио, как самого крупного города, составило ~ 24 млн ( U 0= 24 млн). При стабилизации населения Земли при N ∞ = 11 млрд в будущем население самого крупного города достигнет U ∞ ~ 40 млн.