Сергей Капица - Парадоксы роста. Законы глобального развития человечества

Параметр K определяет не только масштаб численности человечества в начальную эпоху роста, но и дает оценку численности когерентной группы людей или племени как самодостаточной единицы населения. Как большой параметр, постоянная K определяет все соотношения между населением и длительностью процессов роста, а значительная величина константы K приводит к высокой эффективности асимптотических решений. В результате скорость роста населения Земли определяется нелинейным дифференциальным уравнением:

где время τ = T / τ выражено в единицах времени τ и в решениях уравнения (6) отсчитывается от момента прохождения через демографический переход. Характерное время τ одинаково для фазовых переходов в прошлом и настоящем.

Формула роста (6) выражает природу коллективного нелинейного взаимодействия, которое ответственно за рост человечества в эпоху его взрывного развития между двумя сингулярностями. В этом уравнении Т 1и N для усредненных переменных и скорость роста приравнена к развитию, которое равно квадрату численности населения мира, как выражение меры системной сложности населения планеты.

Полное решение должно описывать рост человечества в течение трех эпох. Первая эпоха А– антропогенеза начинается с линейного роста с указанной выше минимальной скоростью. Когда население достигает величины порядка 100 000, наступает эпоха В– взрывного роста со скоростью роста, пропорциональной квадрату населения Земли, и с этого времени человек заселяет всю планету.

Когда скорость квадратичного роста достигла своего предела при удвоении за характерное время τ , наступил кризис мирового демографического роста и переход в эпоху С– стабилизации населения мира. Таким образом, на основании (3) максимальная абсолютная скорость глобального роста во время демографического перехода равна:

при относительном росте:

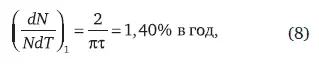
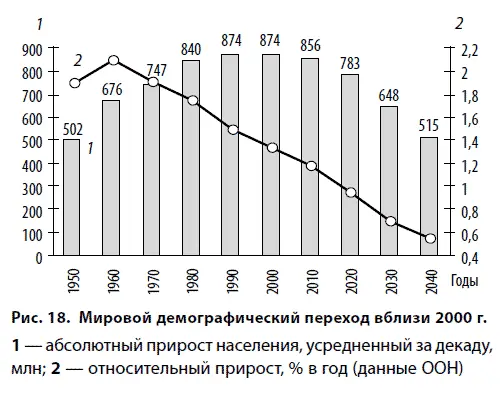
достигнутом в 1995 г., что согласуется с данными ООН, но дает несколько меньшее значение для абсолютной скорости роста при сравнении с табл. 1 (рис. 18).

Население Земли в этот критический момент перехода Т 1= 1995 г. соответственно равно:

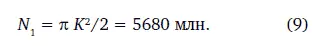
На этой основе легко определить предел N ∞, в два раза больший, чем N 1, к которому в эпоху Сасимптотически стремится население Земли:

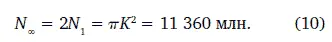
В рамках сделанных предположений это число представляет верхнюю оценку населения Земли в предвидимом будущем. Таким образом, глобальное взаимодействие приводит к ускорению и синхронизации процессов и на заключительной стадии глобального демографического перехода – к сужению перехода и тем самым к снижению предела для населения нашей планеты. Этот результат находится в согласии с интуитивными экстраполяциями демографов. Рассмотрение N (Т) как аналитической функции указывает на асимптотическое поведение при T → ∞, когда N → N ∞, в предположении отсутствия нулей и полюсов в обозримом будущем.

Начальный линейный рост дает оценку времени для эпохи антропогенеза и критической сингулярности в предыстории человечества, которая случилась:

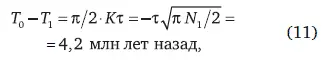
если использовать известное значение для N 1и то же значение τ = 45 лет лет для сингулярности в далеком прошлом и в настоящем. Несмотря на сделанные упрощения, данная оценка вполне согласуется с оценками времени, предложенными для Т 0в антропологии.

Представляет интерес определить полное число людей, живших на Земле. Если переставить переменные в (6) и проинтегрировать:

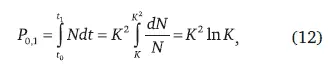
то получим число людей, живших от Т 0до нашего времени Т 1. В оценках других авторов длительность поколения принята равной 20 годам, что ведет к оценке P 0,1= 106 млрд [10]. Поэтому необходимо введение в (12) множителя 45 / 20 = 2,25:

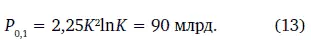
Таким образом, в течение каждого из ln K = 11,00 выделенных периодов жило по 2,25 K 2= 8 млрд людей. Это число является инвариантом для числа людей, живших в экспоненциально сокращающихся циклах.

Эти циклы можно получить, обобщая решение (6) в область комплексных переменных или суммируя экспоненциально сокращающиеся периоды, причем нулевой цикл θ = 0 отвечает линейному росту в течение начальной сингулярности:

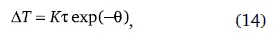
где θ – номер цикла, определить длительность развития при К >>1:

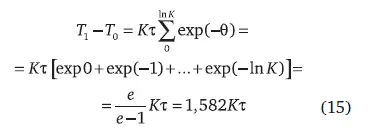
и сравнить ее с (11), где длительность равна:

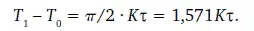
В (15) рост суммируется по гиперболической траектории, во втором случае – по (4):

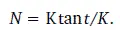
Демографические циклы определяют периодичность развития всего человечества за 4–5 млн лет, включая проходящий по гиперболическому закону рост от конца антропогенеза до наших дней. Наличие выделенных антропологами и историками демографических циклов, как эпох развития человечества, указывает на глобальную устойчивость системы при ее развитии по предельной траектории гиперболического роста.

Для дальнейшего перейдем к переменной n = N/K, когда население Земли измеряется в единицах K :

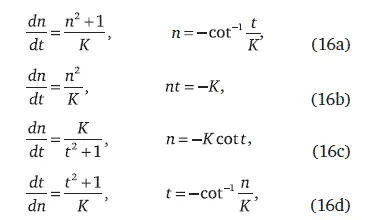
Тогда уравнения для роста становятся симметричными, и это видно по сопряжению переменных n и t . Смена зависимой переменной в (16a) и (16d) происходит при прохождении перехода, когда n становится независимой переменной вместо времени t , что выражено в уравнении роста (3).