Андрей Павлов - Геометрия: Планиметрия в тезисах и решениях. 9 класс
- Название:Геометрия: Планиметрия в тезисах и решениях. 9 класс
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Андрей Павлов - Геометрия: Планиметрия в тезисах и решениях. 9 класс краткое содержание
В пособии конспективно изложен школьный курс геометрии. Приведены комплекты экзаменационных билетов, задачи и их решения, распределённые по различным уровням сложности.
Материалы пособия соответствуют учебной программе школьного курса геометрии.
Для учителей и учащихся 9-х классов.
Геометрия: Планиметрия в тезисах и решениях. 9 класс - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Решение. Обозначим катеты прямоугольного треугольника ABC с гипотенузой ВС через а и b (см. рис). Тогда
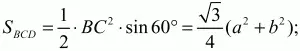
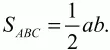
По условию SBCD = 2SABC. Значит,
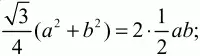
преобразуем это уравнение к виду
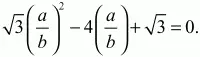
Дискриминант D этого уравнения будет равен
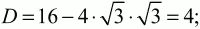

Но a/b = tg(?ВСА), значит, ?ВСА = 60° или 30°.
Ответ: 60°; 30°.
Задача 34 (рис. 234)
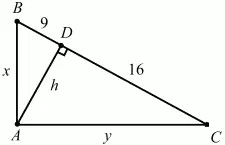
Рис. 234.
Решение. Пусть ABC – заданный треугольник, AD – высота, опущенная на гипотенузу. Тогда по условию BD = 9, DC = 16. Обозначим АВ через х, АС через у, высоту AD через h. По теореме Пифагора: BD2+ AD2= АВ2; DC2+ AD2= АС2; АВ2+ AC2= ВС2. Получаем систему уравнений:
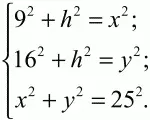
Сложим все уравнения:
81 + 256 + 2h2+ х2+ у2= х2+ у2+ 625;
2h2= 228; h = 12; х2= 81 + 144 = 225; x = 15;
у2= 256 + 144 = 400; y = 20.
Далее воспользуемся формулой r = S/p.
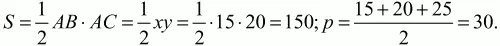
r = 150/30 = 5.
Ответ: 5.
Задача 35 (рис. 235)
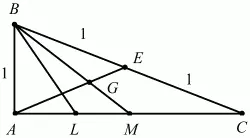
Рис. 235.
Решение. Пусть ABC – данный в условии задачи треугольник. По теореме Пифагора находим, что AC = ?3. Поскольку sin ?ABC = ?3/2, то, учитывая, что угол ?ABC – угол прямоугольного треугольника, находим, что ?ABC = ?/3. Следовательно, ?АСВ = ?/6. Так как BL – биссектриса угла ABC, то ?ABL = ?/6. Из прямоугольного треугольника ABL находим

Пусть М – середина отрезка АС. Тогда AM = 1/2 АС = ?3/2. Из прямоугольного треугольника ВАМ находим, что
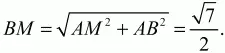
Так как точка пересечения медиан делит каждую из них в отношении 2:1, то
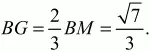
Для ответа на вопрос, поставленный в задаче, надо сравнить числа
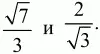
Поскольку
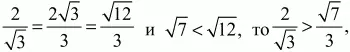
т. е. BL > BG.
Ответ: длина BL больше длины BG.
Задача 36 (рис. 236)
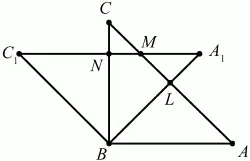
Рис. 236.
Решение. Пусть ABC – данный в условии задачи прямоугольный треугольник, А1ВС1 – прямоугольный треугольник, полученный поворотом треугольника ABC вокруг вершины его прямого угла В на угол 45°. Из условия задачи следует, что величины углов CBC1, CBA1, ABA1, ВСА, ВА1C1 равны 45°. Прямые АВ и А1C1 параллельны, т. к. при их пересечении прямой ВА1 равны накрест лежащие углы АВА1 и ВА1С1. Но тогда, поскольку треугольник ABC прямоугольный и, значит, АВ ? ВС, получаем, что прямая С1А1 перпендикулярна прямой ВС. Обозначим через N точку пересечения прямых С1А1 и СВ. Поскольку
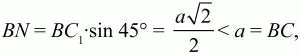
то точка N лежит на отрезке ВС. Пусть L – точка пересечения прямых АС и ВА1. Аналогично показывается, что точка L лежит на отрезке АС. Пусть М – точка пересечения прямых АС и С1А1. Ясно, что точка М лежит на отрезке CL. Тогда SBLMN = SBLC – SCNM. Треугольник BLC равнобедренный и прямоугольный, т. к. в нем ?CBL = ?LCB = 45°. Следовательно,

Треугольник CNM также равнобедренный и прямоугольный, причем
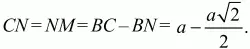
Следовательно,
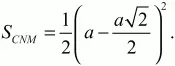
Итак,
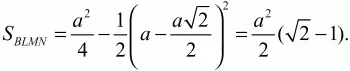
Ответ:
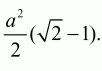
Задача 43 (рис. 237)
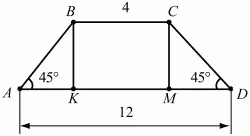
Рис. 237.
Решение. Проведём высоты трапеции ВК и СМ. Очевидно, что КМ = 4; AK = MD = (12 – 4)/2 = 4. Так как треугольник АВК – равнобедренный (?АВК = ?ВАК = 45°). то ВК = АК = 4.
SABCD = (AD + BC)/2 ? BK = (12 + 4)/2 ? 4 = 32.
Ответ: 32 см2.
Задача 44 (рис. 238)

Рис. 238.
Решение. Проведём высоты трапеции ВК и СМ. Мы получили два прямоугольных треугольника АВК и CMD, в которых ?ВАК и ?CDM равны 30°; так как напротив угла в 30° лежит катет (ВК), равный половине гипотенузы (АВ), то АВ = 2h (ВК = h).
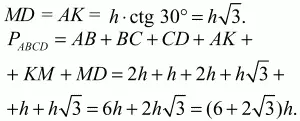
Ответ: (6 + 2?3)h.
Задача 45 (рис. 239)
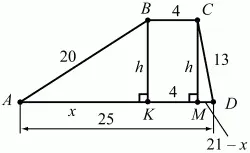
Рис. 239.
Решение. Пусть АК = х, высоты ВК и СМ равны h, тогда, так как КМ = ВС = 4, MD = 21 – х.
Из ?АВК и ?MCD по теореме Пифагора получим:
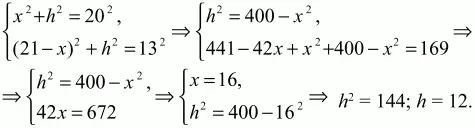
Несложно подсчитать, что если оба угла при нижнем основании не острые, то задача решений не имеет.
Ответ: 12.
Задача 46 (рис. 240)
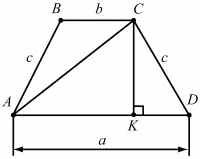
Рис. 240.
Решение. Проведем высоту трапеции СК (см. рис.). Тогда, KD = (a – b)/2; cos D = (a – b)/2c. Из ?ACD по теореме косинусов AC2= AD2+ CD2– 2AD ? CD ? cos D = a2+ с2– 2 ? а ? с ? (a – b)/2c = a2+ с2– a2+ аb = c2+ ab.
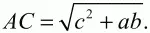
Ответ:
Задача 47 (рис. 241)
Интервал:
Закладка: