Андрей Павлов - Геометрия: Планиметрия в тезисах и решениях. 9 класс
- Название:Геометрия: Планиметрия в тезисах и решениях. 9 класс
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Андрей Павлов - Геометрия: Планиметрия в тезисах и решениях. 9 класс краткое содержание
В пособии конспективно изложен школьный курс геометрии. Приведены комплекты экзаменационных билетов, задачи и их решения, распределённые по различным уровням сложности.
Материалы пособия соответствуют учебной программе школьного курса геометрии.
Для учителей и учащихся 9-х классов.
Геометрия: Планиметрия в тезисах и решениях. 9 класс - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:

Рис. 253.
Решение. Для определённости будем считать, что АВ < AD. Так как AB ? AD = 48 и АВ2+ AD2= BD2= 100, то AD = 8, АВ = 6. Поскольку OB = OD = 13 > BD, то точка О лежит вне круга с диаметром BD и потому вне прямоугольника. Пусть она находится по ту же сторону от диагонали BD, что и точка А. Тогда требуется найти ОС. Обозначим ?OBD через ? и ?DВС через ?. Чтобы найти угол ?, опустим из точки О на диагональ BD перпендикуляр ОК. Получим ВК = KD = 1/2BD. Из прямоугольного ?ОВК следует:
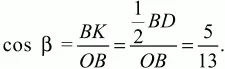
Тогда sin ? = 12/13. Из прямоугольного ?DBС находим:
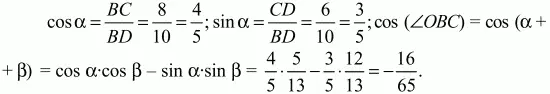
Применяя к треугольнику OBС теорему косинусов, получаем
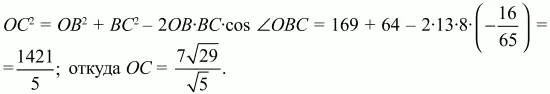
Ответ:
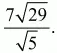
Задача 70 (рис. 254)
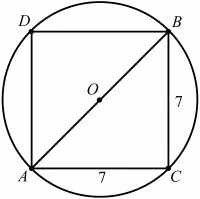
Рис. 254.
Решение. Как видно из рисунка, диаметр окружности d совпадает с диагональю квадрата АВ. По теореме Пифагора
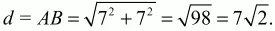
Ответ: 7?2 см.
Задача 71 (рис. 255)
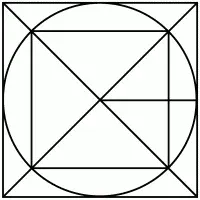
Рис. 255.
Решение. Пусть сторона малого квадрата а, тогда диаметр d = 2Rкруга круга равен диагонали малого квадрата, т. е.

Но Rкруга – это половина стороны большого квадрата. Сторона большего квадрата
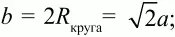
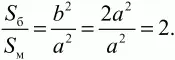
Ответ: 2:1.
Задача 72 (рис. 256)
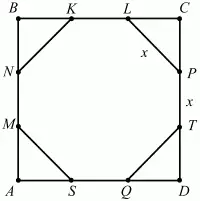
Рис. 256.
Решение. MNKLPTQS – правильный восьмиугольник (см. рис.). Пусть РТ = х, тогда
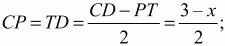
из равнобедренного треугольника LCP
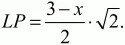
Из равенства LP = РТ получаем:
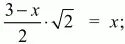
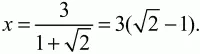
Ответ:
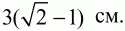
Задача 73 (рис. 257)
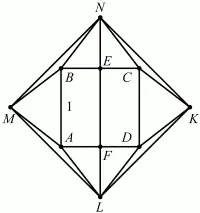
Рис. 257.
Решение. Очевидно, что MNKL – квадрат. Его диагональ NL = NE + FL + EF = 2NE + EF = 2NE + 1 (см. рис.). Так как NE – высота в равностороннем треугольнике BNC, то
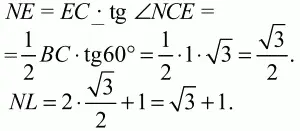
Сторона квадрата
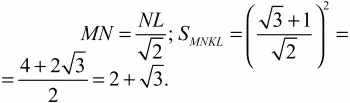
Ответ: 2 + ?3.
Задача 76 (рис. 258)
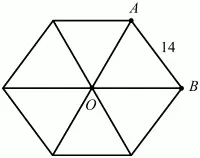
Рис. 258.
Решение. Можно, конечно, пуститься в достаточно длинные арифметические вычисления, но мы покажем самое простое и красивое решение. Раз площадь большого треугольника равна площади шестиугольника, то площадь этого треугольника в 6 раз больше площади треугольника ОАВ. А поскольку площадь правильного треугольника пропорциональна квадрату стороны, то его сторона в ?6 раз больше стороны АВ, т. е. сторона его будет равна 14?6.
Ответ: 14?6.
Задача 77 (рис. 259)
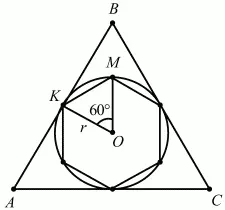
Рис. 259.
Решение. Пусть сторона равностороннего треугольника АВ = a;
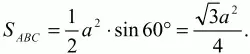
Найдём радиус r вписанной окружности
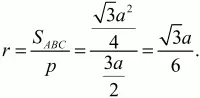
Здесь р = 3a/2 – полупериметр правильного треугольника ABC.
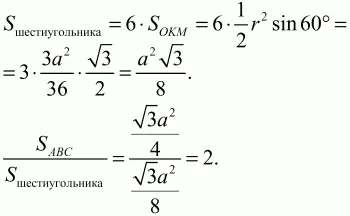
Ответ: 2:1.
Задача 78 (рис. 260)
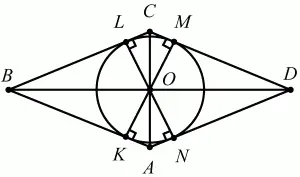
Рис. 260.
Решение. Пусть ABCD – данный четырёхугольник. Обозначим К, L, М, N – точки касания окружности соответственно со сторонами АВ, ВС, CD, AD четырёхугольника ABCD. Соединим эти точки с центром О. Треугольники АОК, AON, CLO, СМО – равны, как имеющие равные гипотенузы и катеты: у них АО = ОС по условию и КО = OL = ОМ = ON = r, где r – радиус окружности, вписанной в четырёхугольник ABCD. Аналогично доказывается, что равны треугольники КОВ, BOL, DON и DOM. Из равенства треугольников имеем, что ?КОВ = ?BOL = ?NOD = ?DOM, а также ?АОК = ?LOC = ?AON = ?СОМ. Значит, ?AON + ?NOD = ?АОК + ?КОВ = ?BOL + ?LOC = ?СОМ + ?MOD. Так как ?АОВ = ?АОК + ?КОВ, ?ВОС = ?BOL + ?LOC, ?COD = ?СОМ + ?MOD, ?AOD = ?AON + ?NOD, то ?АОВ = ?ВОС = ?COD = ?AOD, и поскольку в сумме они составляют 360°, то каждый из них равен 90°. По теореме Пифагора из треугольника АОВ находим, что
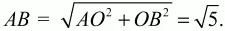
Следовательно, периметр четырёхугольника (ромба) ABCD равен 4?5.
Ответ: 4?5.
Задача 85 (рис. 261)
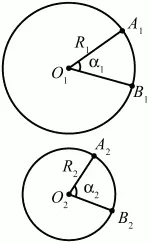
Рис. 261.
Решение. Составим пропорции: ?10? длина дуги А1В1 = 1.
360° ? длина окружности 2?R1. Отсюда
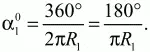
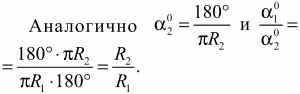
Ответ:
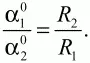
Задача 86 (рис. 262)
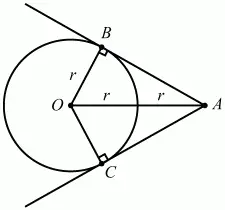
Рис. 262.
Читать дальшеИнтервал:
Закладка: