Андрей Павлов - Геометрия: Планиметрия в тезисах и решениях. 9 класс
- Название:Геометрия: Планиметрия в тезисах и решениях. 9 класс
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Андрей Павлов - Геометрия: Планиметрия в тезисах и решениях. 9 класс краткое содержание
В пособии конспективно изложен школьный курс геометрии. Приведены комплекты экзаменационных билетов, задачи и их решения, распределённые по различным уровням сложности.
Материалы пособия соответствуют учебной программе школьного курса геометрии.
Для учителей и учащихся 9-х классов.
Геометрия: Планиметрия в тезисах и решениях. 9 класс - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Ответ: 66.
Задача 105 (рис. 275)
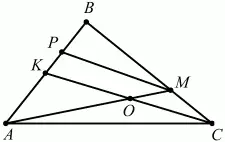
Рис. 275.
Решение. Проведём MP||СК, тогда по теореме о пропорциональных отрезках ВР: РК = ВМ: МС = 3; значит, КР = 1/4 КВ = 1/4 АК и КР: АК = ОМ: АО = 1:4 и АО = 4OМ = 4/5 AM. По условию АК = КВ = 1/2 АВ.
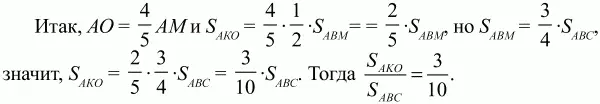
Ответ: 3/10.
Задача 106 (рис. 276)
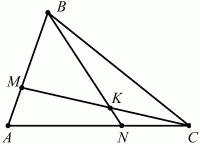
Рис. 276.
Решение. Чтобы найти отношение СК/КМ, применим теорему Менелая к треугольнику АСМ и секущей BN. Получим: CK/KM ? MB/BA ? AN/NC = 1. Так как MB/BA = 2/3, AN/NC = 2, то CK/KM = 3/4.
Аналогично, применив теорему Менелая к треугольнику ABN и секущей СМ, находим BK/KN ? CN/AC ? AM/MB = BK/KN ? 1/3 ? 1/2 = 1, откуда BK/KN = 6.
Ответ: 6; 3/4.
Задача 109 (рис. 277)
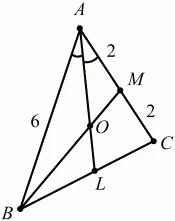
Рис. 277.
Решение. Так как АМ = 2, то по свойству биссектрисы в треугольнике АВМ ВО/OM = АВ/AM = 6/2 = 3.
Ответ: 3.
Задача 110 (рис. 278)
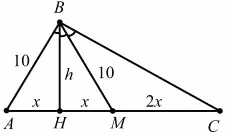
Рис. 278.
Решение. Пусть ВМ – медиана, а ВН – высота в треугольнике. Обозначим ВН через h, МС через 2х. Так как ВН – одновременно биссектриса и высота в треугольнике АВМ, то данный треугольник – равнобедренный и АН = НМ = х, AB = BM = 10. Так как ВМ – биссектриса ?НВС, то BH/BC = HM/MC; h/BC = x/2x; BC = 2h.
Из ?НВМ и ?НВС по теореме Пифагора:
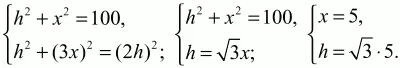
AC = 4x = 20; ВС = 2h = 10?3. Кстати, легко показать, что ?ABC = 90°.
Ответ: 10 см; 20 см; 10?3 см.
Задача 118 (рис. 279)
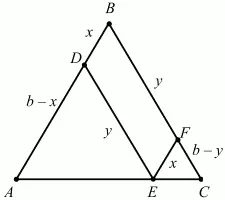
Рис. 279.
Решение. Пусть АС = а; АВ = ВС = b, BF = y, EF = x. ?ADE ~ ?EFC, поэтому FC/DE = FE/DA; (b – y)/y = x/(b – x); b2= by – bx + xy = xy. Отсюда x + у = b; PDBFE = 2(x + y) = 2b, т. е. периметр параллелограмма не зависит от х и y, а зависит только от длины боковой стороны треугольника, другими словами, для данного треугольника периметр вписанного в него параллелограмма есть величина постоянная.
Задача 119 (рис. 280)
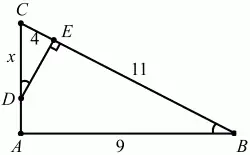
Рис. 280.
Решение. Так как СЕ = 4, то BE = 11. Из ?ABC по теореме Пифагора:
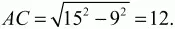
Пусть CD = х. Из подобия ?DCE и ?АСВ CE/AC = CD/CB; 4/12 = x/15; x = 5.
Ответ: 5.
Задача 120 (рис. 281)
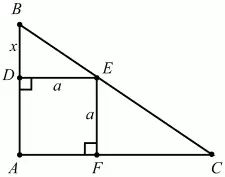
Рис. 281.
Решение. Пусть BD = х, DE = а. Из подобия ?BDE и ?ВАС BD/BE = BA/BC; x/30 = (x + a)/70; 7х = 3х + 3a; x = 3/4a. Заметим, что ADEF – квадрат, т. е. DE = EF = AF = DA = a.
Из ?DBE по теореме Пифагора BD2+ DE2= BE2; х2+ а2= 900; 9а2/16 + a2 = 900; 25а2/16 = 900; а = 24; х = 3/4 ? 24 = 18.
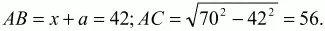
Ответ: 42 см; 56 см.
Задача 121 (рис. 282)
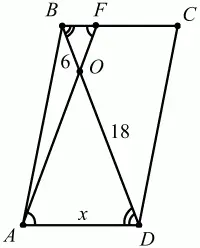
Рис. 282.
Решение. Пусть AD = х. ?BOF ~ ?AOD по равенству трёх углов, поэтому AD/BF = OD/OB; AD/4 = 18/6; AD = 12.
Ответ: 12.
Задача 122 (рис. 283)
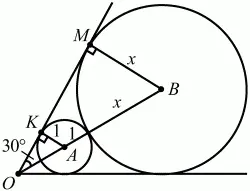
Рис. 283.
Решение. Обозначим радиус большей окружности через х. Из рисунка видно, что из прямоугольного треугольника ОКА ОА = AK/sin 30° = 1/(1/2) = 2. Треугольники OAK и ОВМ подобны, поэтому ОА/OB = АК/BM; 2/(3 + x) = 1/x; 2х = 3 + х; х = 3.
Ответ: 3.
Задача 123 (рис. 284)
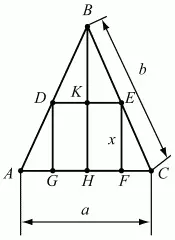
Рис. 284.
Решение. Обозначим сторону квадрата GDEF через х и проведем высоту ВН. ?ВКЕ подобен ?ВНС (см. рис.), значит, BK/KE = BH/HC; (BH – x)/(x/2) = BH/(a/2);
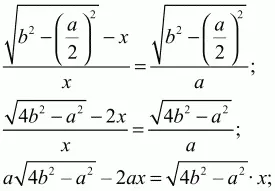
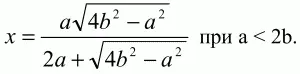
Ответ:
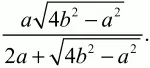
Задача 124 (рис. 285)
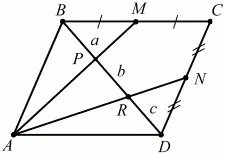
Рис. 285.
Решение. Пусть ВР = a; PR = b; RD = с. ?ВРМ ~ ?APD, значит, ВР/PD = ВМ/AD = 1/2; отсюда b + с = 2а. Аналогично ?RND ~ ?BRA; RD/BR = ND/AB = 1/2; a + b = 2c.
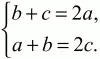
Вычитаем из первого уравнения второе: с – а = 2а – 2с; с = а; а + b = 2с = 2а; а = b.
Ответ: а = b = с, что и требовалось доказать.
Задача 125
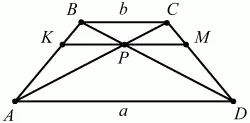
Рис. 286.
Решение. ?РВС подобен ?PAD, поэтому РВ/PD = BC/AD = b/a, PB = PD ? b/a. ?PMD подобен ?BCD, значит РМ/BC = PD/BD;

Ответ: 2ab/(a + b).
Задача 126 (рис. 287)
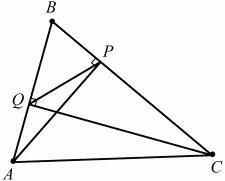
Рис. 287.
Решение. Из прямоугольных треугольников АВР, BCQ находим ВР/AB = cos В, BQ/BC = cos В. Из этих равенств следует, что треугольники BPQ и ABC подобны (по двум сторонам и углу между ними), причём коэффициент подобия равен cos В. Так как отношение площадей подобных многоугольников равно квадрату коэффициента подобия, то
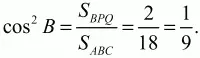
По условию треугольник ABC остроугольный, значит, cos В > 0 и, следовательно, cos В = 1/3. Из подобия треугольников ABC и BPQ вытекает равенство

Обозначим через R радиус окружности, описанной вокруг треугольника ABC. По теореме синусов:
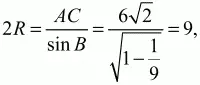
откуда R = 9/2.
Ответ: R = 9/2.
Задача 129 (рис. 288)
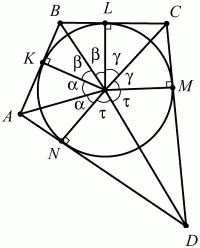
Рис. 288.
Решение. Соединим центр окружности О с вершинами четырёхугольника и точками касания. Перед нами четыре пары равных треугольников: ?АОК = ?AON. ?ВОК = ?BOL, ?COL = ?COM, ?DOM = ?DON. Тогда ?АОК = ?AON, ?ВОК = ?BOL, ?COL = ?COM, ?DOM = ?DON. Из рисунка видно, что 2? + 2? + 2? + 2? = 360°, ? + ? + ? + ? = 180°. ?АОВ + ?COD = ? + ? + ? + ? = 180°.
Читать дальшеИнтервал:
Закладка: