Андрей Павлов - Геометрия: Планиметрия в тезисах и решениях. 9 класс

Рис. 241.

Решение. По содержанию задача идентична задаче 45. Однако, если мы начертим аналогичную трапецию и введем 25 соответствующие обозначения, то из чертежа получится система:

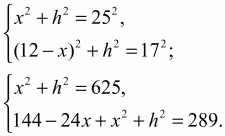
24х = 144 + 625–289 = 480; х = 20. Получается, что MD = 12–20 = -8. Это лишь означает, что трапеция выглядит как на рис. 242:

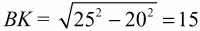
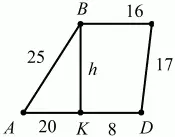
Рис. 242.

Ответ: 15 см.

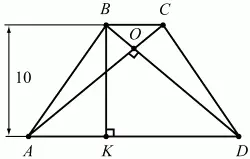
Рис. 243.

Решение. Так как ABCD – равнобедренная трапеция, то АО = OD и ?OAD = ?ODA = 45°. Проведём высоту BK (см. рис.). Раз ?ODA = 45°, то ?KBD – равнобедренный и KD = BK = 10.

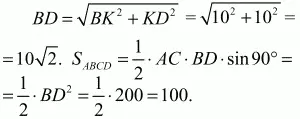
Ответ: 100.

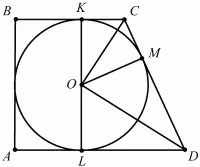
Рис. 244.

Решение. Пусть ABCD – данная в условиях задачи трапеция. Обозначим через точку М точку касания окружности со стороной CD трапеции ABCD. Соединив точки С и D с центром окружности, получим треугольник COD. Так как точка О равноудалена от прямых ВС и CD, то СО – биссектриса угла BCD и ?OCD = 1/2 ?BCD. Аналогично, ?ODC = 1/2 ?ADC. Поскольку BC||AD, то ?BCD + ?ADC = ?, следовательно, ?OCD + ?ODC = ?/2. Тогда ?COD = ?/2, т. е. треугольник COD – прямоугольный. По теореме Пифагора

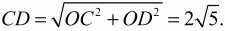
Так как M – точка касания окружности и стороны CD, то CD ? ОМ. Из подобия прямоугольных треугольников OCD и OMD (они имеют общий острый угол) находим, что CD/OD = OC/OM.

Отсюда

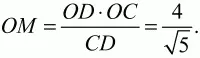
Проведём через точку О прямую, перпендикулярную ВС. Тогда она будет перпендикулярна и прямой AD. Поскольку такой перпендикуляр к прямым ВС и AD единственен, то точки пересечения его L, K c прямыми AD и ВС соответственно будут точками касания сторон трапеции с окружностью. Значит, длина высоты трапеции равна KL = 2 ? ОМ = 8/?5 и АВ = 8/?5. Поскольку в четырехугольник ABCD вписана окружность, то BC + AD = AB + CD = 18/?5. Откуда SABCD = 1/2(BC + AD) ? AB = 72/5.

Ответ: 72/5.

Рис. 245.

Решение. Исходя из условия задачи, получим систему:

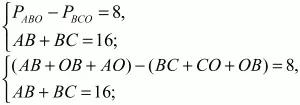
Учитывая, что AO = СО, получим:

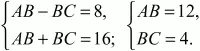
Ответ: 12 см; 4 см; 12 см; 4 см.

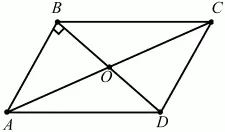
Рис. 246.

Решение. Так как по условию BD = 6, АС = 2?22, то, учитывая, что диагонали параллелограмма точкой пересечения делятся пополам, получим: АО = ?22, ВО = 3. Из прямоугольного треугольника АВО по теореме Пифагора

Из прямоугольного треугольника ABD

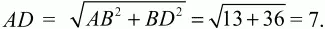
Ответ: 7.

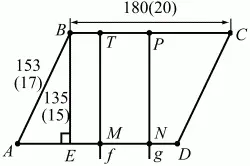
Рис. 247.

Решение. С целью упрощения арифметических вычислений уменьшим все линейные размеры в 9 раз. Тогда АВ = 17; ВС = 20; BE = 15. Линии f и g делят площадь трапеции на три равные по площади части (см. рис.). Проведем высоту BE. Последовательно находим: SABCD = AD ? BE = 20 ? 15 = 300 (в «новом формате»).

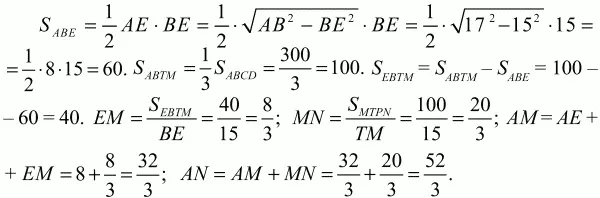
Осталось увеличить полученные результаты в 9 раз: AM = 96; AN = 156.

Ответ: 96; 156.

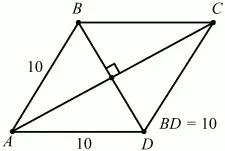
Рис. 248.

Решение. Пусть в ромбе ABCD BD = АВ = AD. Тогда ?ABD – равносторонний и АВ = ВС = 10, ?BAD = 60°, ?АВС = 120°. По теореме косинусов из треугольника ABC

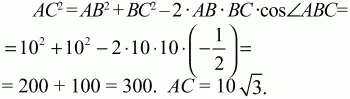
Ответ: 10?3 см; 120°; 60°.

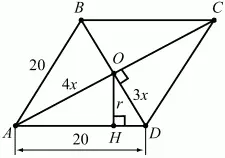
Рис. 249.

Решение. Начертим ромб ABCD. По условию

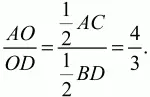
Так как диагонали ромба перпендикулярны друг другу, то ?AOD – прямоугольный. Тогда по теореме Пифагора АО2+ OD2= AD2. Обозначим АО через 4х, тогда OD = Зх.

(4х)2+ (Зх)2= 202; 25х2= 400; х2= 16; х = 4. АО = 16; OD = 12. Осталось найти высоту ОН в ?AOD, которая и является радиусом вписанного круга. Из рисунка

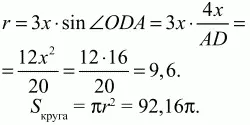
Ответ: 92,16? см2.

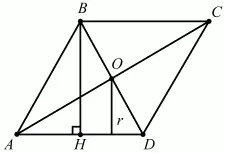
Рис. 250.

Решение. Во-первых, раз

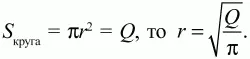
Во-вторых, высота ромба равна диаметру вписанного круга, значит,

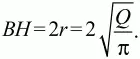
Так как

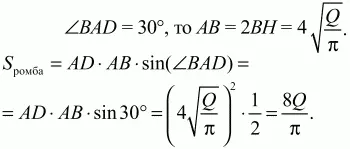
Ответ: 8Q/?.

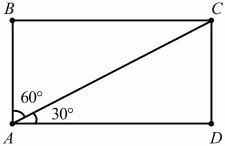
Рис. 251.

Решение. Так как ?BAC/?CAD = 1/2, а ?ВАС + ?CAD = 90°, то ?ВАС = 60°, ?CAD = 30°. Из ?ACD CD = AD ? tg 30° = AD/?3. Тогда CD: AD = 1:?3.

Ответ: 1:?3.

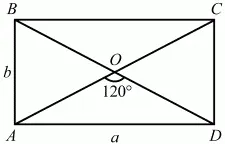
Рис. 252.

Решение. Пусть AD = а, АВ = b. По условию SABCD = а ? b = 9?3.

Так как ?AOD = 120°, то ?BOA = 60°. Значит, ?АОВ – равносторонний и OB = b; BD = 2b. Из ?ABD а2+ b2= (2b)2; а = ?3b. ?3b ? b = 9?3; b = 3; а = 3?3.

Ответ: 3 см; 3?3 см.