Андрей Павлов - Геометрия: Планиметрия в тезисах и решениях. 9 класс
- Название:Геометрия: Планиметрия в тезисах и решениях. 9 класс
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Андрей Павлов - Геометрия: Планиметрия в тезисах и решениях. 9 класс краткое содержание
В пособии конспективно изложен школьный курс геометрии. Приведены комплекты экзаменационных билетов, задачи и их решения, распределённые по различным уровням сложности.
Материалы пособия соответствуют учебной программе школьного курса геометрии.
Для учителей и учащихся 9-х классов.
Геометрия: Планиметрия в тезисах и решениях. 9 класс - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Ответ: 180°.
Задача 130 (рис. 289)
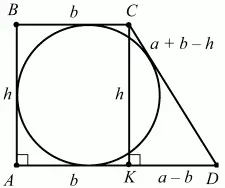
Рис. 289.
Решение. Так как в трапецию можно вписать окружность, то АВ + CD = AD + ВС. Если АВ = h; AD = a; BC = b, то CD = a + b – h, KD = а – b. Из треугольника KCD следует, что KD2+ CK2= CD2; (а – b2) + h2= (a + b – h2). Имеем: a2 – 2ab + b2+ h2= a2+ b2+ h2+ 2ab – 2ah – 2bh; -2ab = 2ab – 2ah – 2bh; ah + bh = 2ab; h = 2ab/(a + b). h – диаметр окружности.
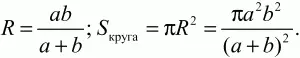
Ответ:
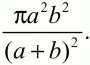
Задача 131 (рис. 290)
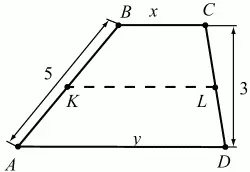
Рис. 290.
Решение. Пусть ABCD – данная трапеция, АВ = 5, CD = 3, KL – средняя линия. Обозначим величины отрезков ВС и AD через х и у соответственно. Так как в четырёхугольник ABCD можно вписать окружность, то х + у = ВС + AD = АВ + CD = 8. Поскольку KL – средняя линия трапеции, то KL = (BC + AD)/2 = 4. Если h – высота трапеции ABCD, то из теоремы о пропорциональных отрезках, отсекаемых параллельными прямыми, следует, что высоты трапеций KBCL и AKLD равны h/2. Для площадей этих трапеций имеем
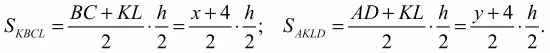
По условию
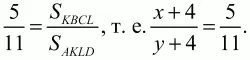
После упрощений получаем уравнение 11x – 5у = -24. Система уравнений

имеет единственное решение х = 1, y = 7.
Ответ: BC = 1, AD = 7.
Задача 135 (рис. 291)
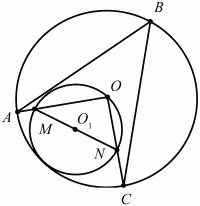
Рис. 291.
Решение. По теореме о величине вписанного в окружность угла ?ABC = 1/2 ?АОС. Заметим, что ?АОС = ?MON, a yroл ?МОN опирается на диаметр MN окружности с центром О1. ?АОС = 90°, и значит 1/2 ?АОС = 1/2 90° = 45°.
Ответ: 45°
Задача 136 (рис. 292)
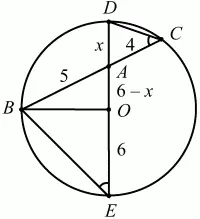
Рис. 292.
Решение. Пусть точка А делит хорду ВС на отрезки 5 и 4. Проведём через точки А и О (центр окружности) диаметр ED, причём ED = 2R = 12. Обозначим AD через х, тогда ОА = 6 – х (см. рис.). ?DCA = ?АЕВ (опираются на одну и ту же дугу BD), ?ADC подобен ?BEА (по двум углам), значит, AD/AB = AC/AE; x/5 = 4/(12 – x); 12х – х2= 20; х2 – 12х + 20 = 0; х = 10 или 2. Учитывая, что х ? R, получим x = AD = 2.
Ответ: 2.
Задача 137
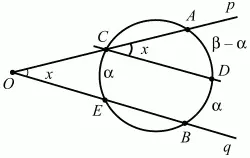
Рис. 293.
Решение I (рис. 293). Обозначим точки пересечения окружности лучами р и q соответственно через С, А и Е, В. Проведём CD||ЕВ. Получим угол ?ACD = х. Угол ?ACD является вписанным в окружность и по определению равен половине дуги AD. По условию задачи дуга СЕ = ?, а дуга АВ равна ?. Тогда дуга AD = ? – ?. В таком случае х = 1/2 (? – ?).
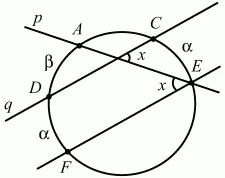
Рис. 294.
Решение II (рис. 294). Обозначим точки пересечения окружности прямыми р и q соответственно через А, Е и D, С. Проведём EF||CD. Угол AEF будет равен х (как внутренние накрест лежащие углы при параллельных CD, FE и секушей АЕ). ?AEF является вписанным в окружность и равен половине дуги AF. Из условия задачи и построений следует, что дуга AF = ? + ?.
Следовательно,
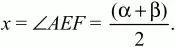
Задача 138 (рис. 295)
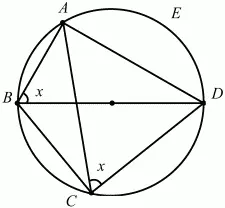
Рис. 295.
Решение. Так как BD – диаметр окружности, то ?BAD = ?BCD = ?/2. Обозначим ?ABD через х, тогда из прямоугольного треугольника ABD получаем, что cos х = AB/BD. По условию BD = 2, АВ = 1, значит, cos х = 1/2, и так как х – внутренний угол прямоугольного треугольника ABD, то х = ?/3. Тогда ?DBC = 3/4 (?ABD) = 3/4 ? ?/3 = ?/4. Вписанные углы ACD и ABD опираются на одну и ту же дугу AED, значит, ?ACD = ?ABD = ?/3. Из треугольника ADC по теореме синусов получаем, что
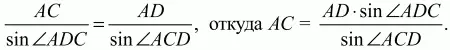
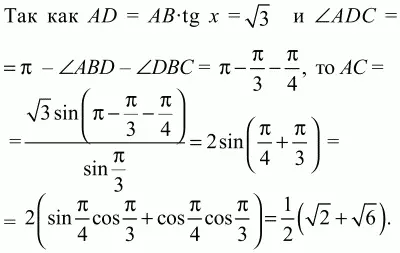
Ответ:
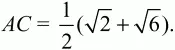
Задача 141
Решение. OB = 4; ВС = 3, значит ОС = 7. OB ? ОС = ОА2; 4 ? 7 = OA2; OA = 2?7.
Ответ: 2?7.
Задача 146 (рис. 296)
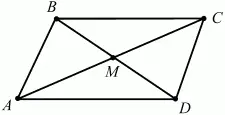
Рис. 296.
Решение. Достроим ?ABD до параллелограмма. Тогда АС < АВ + ВС, но АС = 2AM, 2AM < АВ + ВС = АВ + AD, что и требовалось доказать. Заметим, что AM является медианой ?ABD.
Задача 147 (рис. 297)

Рис. 297.
Решение. Достаточно построить симметричные точки относительно берегов и длина полученной ломаной равна длине прямолинейного отрезка А'В', т. е. минимальна.
Задача 148 (рис. 298)
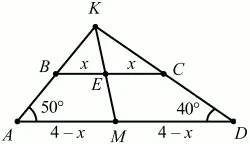
Рис. 298.
Решение. Так как средняя линия трапеции ABCD равна 4, то сумма оснований равна 8. Воспользуемся тем, что середины оснований и точка пересечения боковых сторон трапеции лежат на одной прямой КМ. Из ?AKD ?AKD = 90°. Заметим, что ?AKD – прямоугольный, причем AD – гипотенуза и точкой М делится пополам. Но тогда AM = MD = КМ = 4 – х (радиусы описанной около ?AKD окружности), КЕ = 3 – х, где х – это длина отрезков BE и ЕС. Из подобия ?АКМ и ?ВКЕ следует: (4 – х)/x = (4 – х)/(3 – x); x = 3/2; BC = 3, AD = 5.
Ответ: 5 и 3.
Задача 154 (рис. 299)
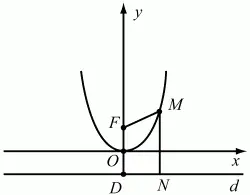
Рис. 299.
Решение. Пусть D – проекция точки F на прямую d. Середину О отрезка DF примем за начало прямоугольной системы координат, а прямую OF – за ось ординат. Точке F отнесём координаты (0; 1). Прямая d будет иметь уравнение у = -1. Пусть М(х; y) – произвольная точка плоскости. Тогда

и MN = |у + 1 |, где MN – расстояние от точки М до прямой d. Если
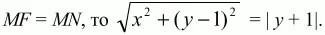
Возведя обе части в квадрат, получим уравнение у = 1/4x2.
Читать дальшеИнтервал:
Закладка: