Андрей Павлов - Геометрия: Планиметрия в тезисах и решениях. 9 класс

3) 5 см (воспользоваться подобием ?DCE и ?АСЕ).

4) Воспользоваться теоремой Фалеса.

3) Воспользуйтесь свойством параллельных прямых.

4) Учесть то, что треугольник разбивается на прямоугольник и два равнобедренных треугольника (значит, сторона прямоугольника равна катету малого треугольника). Периметр равен сумме катетов.

3) 12 см (?BOF ~ ?AOD).

4) Докажите, что расстояния от точки пересечения диагоналей до сторон ромба равны.

3) Докажите равенство углов DBA и ACF и воспользуйтесь признаком параллельности прямых.

4) Выразите по теореме Пифагора квадрат каждой стороны четырёхугольника через соответствующие отрезки диагоналей.

3) 68°, 68° и 44°.

4) 4?3 см и 6?2 см.

3) 4 (т. к. 180° (n – 2) = 360°).

4) Если АС = а, то AD = a/2, АВ = 2а, DB = 3a/2.

3) 56 см.

4) В равностороннем треугольнике биссектрисы и медианы совпадают; воспользуйтесь свойством точки пересечения медиан.

3) 66° и 66°.

4) По 60°.

3) 8, 6 и 6 см.

4) 60° (угол DOG, больший 180°, равен 2 ? 150° = 300°).

3) 13 см.

4) Стороны равностороннего треугольника – по 12 см, а равнобедренного – 12, 14 и 14 см.

3) Треугольники равны по двум сторонам и углу между ними.

4)

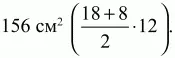
3) Треугольники равны по двум сторонам и углу между ними.

4) 1:1:?3.

3) 5 см (обозначьте АВ = ВС = a; AD = DC = в, BD = х и запишите систему уравнений).

4) 12 и 8 см (докажите равенство ?AMP и ?PNC, из которого следует, что АР = 12).

3) 67°.

4) Воспользуйтесь тем, что внешний угол треугольника равен сумме двух внутренних, с ним не смежных.

3) 25/2 см2.

4) 5 (т. к. сумма внешних углов равна 360°, то угол в правильном многоугольнике равен 468° – 360° = 108°. Далее: 180°(n – 2)/n = 108°; n = 5).

3) Пусть АВ – общая хорда двух окружностей с центрами О1 и O2, ?О1АO2 = ?О1BO2 (по трем сторонам), значит, углы АO2О1 и O1O2B равны, а биссектриса в равнобедренном треугольнике является и высотой.

4) 16 (т. к. в трапецию вписана окружность, то сумма оснований – а она равна 8 – равна сумме боковых сторон).

3) Увеличивается на 20? см.

4) Проведите диагонали в трапеции, рассмотрите средние линии полученных треугольников и учтите равенство боковых сторон трапеции.

3) С(0; -6).

4) 20 см.

3) Медиана в равнобедренном треугольнике является и серединным перпендикуляром.

4) Окружность (середины равных хорд окружности равноудалены от центра окружности).

3) 37,9 дм.

4)

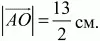
5) 12 см.

3) 12 и 8 см.

4) а) 6 см; б) 8 см; нет.

5) К (18, 12).

3)

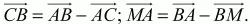
4) б) 80° и 100°.

5) Докажите равенство ?AFC и ?АМС.

3) 41° и 49°.

4) а) угол D = 30°, угол CAD = 15°; б)

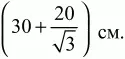
5) 210 см2.

3) 4 и 3 см (воспользуйтесь свойством биссектрисы).

4) 6 см.

5) Уменьшится в 21 раз.

3) Получится равная трапеция.

4) 25?2 см2.

5) Докажите равенство ?АОВ и ?EOD.

3) 53° (ВС параллельна AD).

4) x = 2; y = -0,5;z = -1.

5)

(пусть

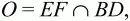
далее для нахождения ЕО и OF воспользуйтесь теоремой синусов).

3)

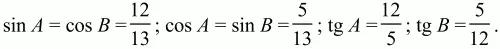
4) 60 см2.

5) 15° (?АВР – равнобедренный, а т. к. угол В равен 50°, то угол PAC = 65° – 50° = 15°).

3) Да.

4) (9 + 3?3) см.

5) 60° (угол ВАО равен углу СВО и пусть он равен ?;

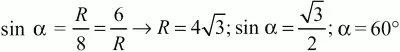
и угол ВОС равен 180° – 60° – 60° = 60°).

з) ?3.

4) ?7 см.

5) 10/?7 = (по теореме косинусов третья сторона равна ?21, значит

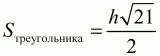
и т. д.).

3) 32° (СО – часть высоты).

4) 15 и 24 м.

5) Докажите, что ?MDP = ?NBK, ?ANM = ?КСР и воспользуйтесь признаком параллелограмма).

3) 73°.

4) 30?2 см2.

5)

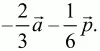
3) 40?3 см2.

4) Нет, т. к. треугольника со сторонами 1, 4 и 5 не существует (сумма двух любых сторон треугольника всегда больше третьей стороны).

5) 5 см (достройте трапецию до правильного шестиугольника).

3) Да (k = 2).

4) 4?3 + 6.

5) 62°, 49°, 69°.

3) 43°.

4) DE = 96/5 м (проще всего заметить, что ?ADE ~ ?ABC).

5) 22 см.

3) 12; 12?3; 24 см.

4) а) равенство следует из подобия треугольников ВНС и DCP.

б) 4/5.

5) Проведите из центра квадрата прямые, параллельные сторонам квадрата и найдите равные треугольники.

3)

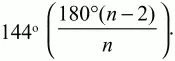
4) а) МТ и РК параллельны, a MP и КT – нет; б) да.

5) 110° и 70°.

3) Угол DBC равен 17°, угол ABC равен 34°, АС = 18 см.

4) а) 0; б) – 2 (угол между векторами 120°).

5) 2, 3, 4, 5 или 6 см.

3) ?3a2/4 (задача 99; см. решение на стр. 155).

4) 84° (задача 133).

3) 3(?2–1) (задача 72; см. решение на стр. 149).

4) 100 (задача 48; см. решение на стр. 144).

3) 5 (задача 75).

4) (задача 167; см. решение на стр.167).

3)

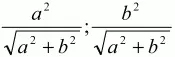
(задача 140).

4) 6 (задача 103).

3) 12 и 4 (задача 53; см. решение на стр. 145).

4) 2 (задача 136; см. решение на стр.162).

3) 3/2 (задача 81).

4)

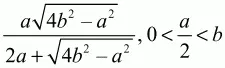
(задача 123; см. решение на стр.158).