Андрей Павлов - Геометрия: Планиметрия в тезисах и решениях. 9 класс

Обратно, если координаты точки М удовлетворяют этому уравнению, то х2= 4у и, следовательно,

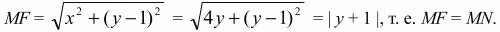
Заметим, что если вместо DF = 2 положить DF = р, то получим уравнение х2= 2ру.

Из школьного курса алгебры известно, что линия, определяемая уравнением у = ах2, называется параболой.

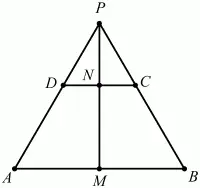
Рис. 300.

Решение. Переведём условие задачи на векторный язык. Поскольку точки Р, A, D так же, как и точки Р, В, С, лежат на одной прямой, то PD = аРА, PC = bРВ, где а и b – коэффициенты пропорциональности, а > 0; b > 0. Точки М и N – середины отрезков АВ и CD. Следовательно,

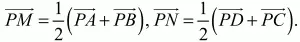
Учитывая приведённые выше равенства, получаем: PN = 1/2(аРА + bРВ). Согласно условию задачи, векторы РМ и PN коллинеарны. Следовательно, найдётся такое число ?, что

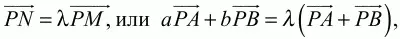
откуда (а – ?)РА + (b – ?)РВ = 0. На основании единственности разложения вектора по неколлинеарным векторам РА и РВ заключаем, что а = b = ?. Таким образом, PD = аРА и PC = аРВ. Вычитая из первого равенства второе, получаем CD = аВА. Значит, стороны CD и АВ параллельны, т. е. ABCD – трапеция.

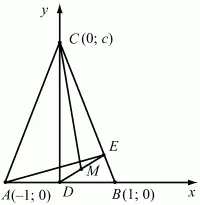
Рис. 301.

Решение. Высота равнобедренного треугольника является его осью симметрии. Поэтому середину D основания АВ треугольника ABC удобно принять за начало прямоугольной системы координат, а направленные прямые АВ и DC – за оси координат. Тогда вершинам треугольника можно отнести координаты: А(-1; 0), B(1; 0), С(0; с).

Вычислим угловые коэффициенты прямых АЕ и СМ. Для этого сначала найдём координаты точек Е и М. Запишем уравнение прямой ВС: х + у/с = 1 или у = – сх + с.

Так как DE ? ВС, то угловой коэффициент прямой DE равен 1/с, а её уравнение есть у = (1/c)x. Решая систему уравнений

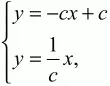
находим координаты точки Е:

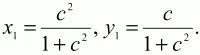
Следовательно, М (х1/2; у1/2).

Угловые коэффициенты прямых АЕ и СМ равны соответственно

Подставив значения x1 и у1 получим:

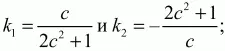
k1k2 = -1, что говорит о перпендикулярности прямых. Значит, отрезки АЕ и СМ перпендикулярны.

Решение. Имеем (PA + РВ + PC)2? 0, причем равенство достигается только тогда, когда Р – центроид треугольника ABC. Отсюда

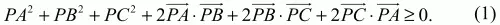
Но

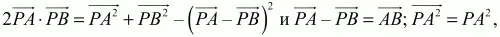
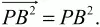
Тогда

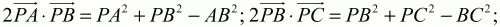
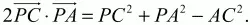
Подставив эти значения скалярных произведений в неравенство (1), получим:

Рис. 302.

Решение. Пусть ЕК = КМ = MF = а. ЕК – средняя линия в ?ABC, значит, ВС = 2а. ЕМ – средняя линия в ?ABD, поэтому AD = 2ЕМ = 2 ? 2а = 4а; AD/BC = 4а/2а =2.

Ответ: 2:1.

Рис. 303.

Решение. NK и MP – средние линии в ?BCD и ?ABD, поэтому NK||BD и MP||BD; MP = 1/2 BD и NK = 1/2 BD. Значит, MP||NK и MP = NK. Аналогично MN||PK (||AC) и MN = PK = 1/2 AC. Так как трапеция равнобедренная, то АС = BD, значит MN = NK = КР = РМ. Параллелограмм MNKP – ромб.

Рис. 304.

Решение. Очевидно, что MNPQ – параллелограмм. ?BAD + ?ABC = 180°. Так как AM и ВМ – биссектрисы, то ?ВАМ + ?АВМ = 90°, значит, ?АМВ = 90° и ?NMQ = 90°. Таким образом, MNPQ – прямоугольник.

Рис. 305.

Решение. SABCD = 1/2 BD ? AC ? sin ? = S. Sпараллелограмма = ab sin ? = BD ? AC ? sin ? = 2S.

Ответ: 2S.

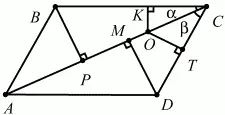
Рис. 306.

Решение. Обозначим точку на диагонали, о которой идет речь в условии задачи, через О. Так как ?ABC = ?ACD, то равны и высоты ВР и DM этих треугольников. ОК = ОС ? sin ?; ОТ = ОС ? sin ? (см. рис).

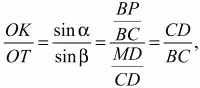
что и требовалось доказать.

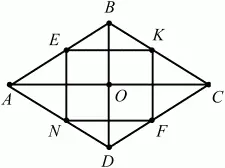
Рис. 307.

Решение. Пусть ABCD – данный в условии задачи четырёхугольник. Обозначим через Е, К, F, N середины сторон АВ, ВС, CD и AD соответственно. Тогда EN – средняя линия треугольника ABD, и, значит, EN||BD. Аналогично доказывается, что KF||BD, ЕК||АС и NF||АС. Это означает, что EN||KF и ЕК||NF, т. е. четырёхугольник NEKF – параллелограмм. По свойству параллелограмма ЕК = NF. EN = KF, и по условию EF = NK. Отсюда следует, что четырёхугольник NEFK – прямоугольник. Ранее доказано, что EN|| BD и ЕК||АС, поэтому BD ? AC. SABCD = 1/2 ? AC ? BD ? sin90° = 1/2 ? 2 ? 1 ? 1 = 1.

Ответ: 1 м2.

3) 74°.

4) ?1/?2 = R2/R1.

3) 94 см.

4) AB + BD + DC = 14 см.

3) 12? см2.

4) Воспользоваться тем, что две крайние части средней линии трапеции равны половине верхнего основания.

3) 4 и 6 см.

4) Если В1К1С – точки касания (К – точка касания окружностей), О1, О2 – центры окружностей, то сначала доказываем, что ?АО1К = ?АКO2, а затем, что ?ВАО1 = ?АO2С.