Абрахам Меррит - Мир приключений, 1929 № 05-06

Издатель: Изд-во «П. П. Сойкин»　

Редактор: Редакционная Коллегия　

Ленинградский Областлит № 85229.　

Тип. ЛСПО. Ленинград, Лештуков, 18.　

Зак. № 1299. Тираж 30.000 экз.　

Редактирует ЗАГАДАЙ-КА.

Конкурс небольшой — участвовало 22 подписчика. В зачет получили: 2 чел. — по 8½ очков, 5 — по 7½ очков, 1–7 очков, 2 — по 6½ очков и остальные — меньше. Премии распределены так:

1-я премия. «Бахчисарайский фонтан» А. С. Пушкина. художеств, издание, — Б. И Скрябин (Москва).

2-я премия. Бесплатное получение в 1929 г. журнала «Вестник Знания» — С. С Батуев (Серпухов).

3-я и 4-я премии. «Гений и творчество» проф. Грузенберга — В. Л. Воронцовский (Тула) и Толстоногов (Баку).

5-я—10-я премии. Любые из издании, указанных в условиях конкурса. 5) Э. Эллер (Новосокольники); 6) Б. В. Смирнов (Одесса); 7) М. Г. Грикуров ; 8). Л. А. Лещенко, 9) А. А. Колосов (Москва); 10) В. М. Николаев.(Грозный).

Первая половина задачи имеет бесконечное число решений, при наименьшем числе долей квадрата, равном 5. Способ решения таков (см. ф. 1). Из угла квадрата А. проводится любая секущая AF, пересекающая правую сторону квадрата в ее верхней полов и и о, напр. р точке С. Прямая BD, параллельная AF, пересекает правую сторону квадрата в точке D, точка О — середина линии DC. Прямая EF проводится через О так, что угол CFE — углу ВАС. Нетрудно доказать, что равнобочная трапеция ABEF равновелика данному квадрату (помимо общей их части, у них равны заштрихованные четырехугольники и светлые треугольники МСУ и ОСF — причем CN = ОС и СМ = СР).

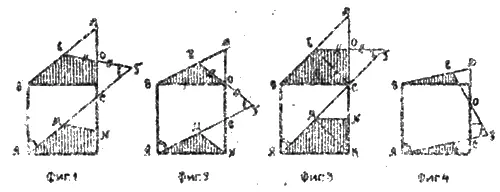
На фиг. 2 и 3 изображены решения при крайних положениях секущей: на фиг. 2 точка С находится в середине стороны квадрата, а на фиг. 3 — в противоположном углу квадрата (все буквенные обозначения остаются прежние). Для таких предельных случаев легко определить величину углов трапеции (в последнем случае углы при большом основании очевидно равны 45°; здесь возможно и другое деление квадрата по долям, если вместо MN провести МК). Верное геометрическое решение получается и в том случае, если секущая АС пересечет противоположную сторону ниже ее середины (фиг. 4.) но такое решение не удовлетворяет требованиям задачи, так как при нем получается в квадрате и в трапеции по 4 доли вместо трех. Предлагаем самим читателям продолжить и закончить исследование такого решения при различных положениях точки С на продолжении правой стороны квадрата (см. фиг. 5)

Для второй половины задачи есть тоже очень много решений — при том же числе дробимых долей. Одним из наиболее простых будет тот случай, когда высота трапеция берется равной удвоенной стороне или половине стороны квадрата (см. фиг. 6 и 7)

Вагон оборудован нецелесообразно, так как все бидоны, прислоненные к стенкам за ними (считая по направлению движения поезда) будут при резких торможениях или остановках скидываться вниз. Целесообразнее делать стелажи не поперек вагона, а вдоль его. — Для робких пассажиров, ездящих в поездах курьерских и тихоходах, есть некоторый смысл выбирать вагоны в первом случае в хвосте поезда (их меньше шансов нагнать сзади), а во втором случае — в голове поезда. Применительно к молоку, независимо от шансов на крушение, для обезопасения от толчков при резких торможениях или остановках лучше садиться спиной к направлению движения (лежать на нижних полках сравнительно безопаснее, чем на верхних).

Старик выяснил сперва, что в подземелье ость строго прямолинейный путь. Для этого он сделал проверку: спустившись в колодце, он оставил у стены зажженный фонарь, а затем поднялся, обошел по горе к выходу, и, войдя в подземелье, убедился, что свет фонаря ясно виден с того примерно места, где на схеме пунктирный проход делает поворот под прямым углом. Пройдясь потом по подземелью до колодца, строго держась все время на свет фонаря, он нащупал в самом конце, справа от себя, выступ степы ближайшей к колодцу пещеры и тщательно измерил расстояние от этого выступа до фонаря. При дальнейших спусках в подземелье, старик всегда ставил свой фонарь строго на прежнее-же место у стены и, пятясь от него назад, без особых трудов доходил до первого выступа стены (тоже справа от себя): а после того он преходил тем-же рачьим способом и весь путь, проверяя все время створу темного выступа степы на освещенный фонарь. Для удобства обратного следования по подземелью, он стал ставить еще в самом угле поворота маршрута зеркальце, чтобы свет фонаря отражался-бы при самом входе в подземелье из долины.

Если обозначить через а гипотенузу данного треугольника, через А— тот катет, в сторону которого делается построение, через с — второй катет и через h1, h2, h3 и т. д. — последовательно все проводимые перпендикуляры, то можно написать такие пропорции: h1: с = b: с; h2: h1 = b: а; h2: h3 = b: a; h1: h3 = b: a и т. д. Отсюда ясно, что ряд h1, h2, h3, h4, .…. представляет собой бесконечно убывающую геометрическую прогрессию, знаменатель которой есть Ь: а (меньше 1). Сумма такой прогрессии как доказывается в алгебре, равняется частному от делению первого члена прогрессии на разность между единицей и знаменателем прогрессии. Значит: h1+h2+h3+h4 +….. = (bс: а):(1-b: а) = bс: (а-b). По условию последняя величина равняется периметру a+b+с. Из ур-ний:

1) a+b+c = bс: (a-b) и 2) а 2 = b 2+с 2 находим соотношения между сторонами: это можно сделать, напр., после приравнения одной стороны, напр. а, к единице. Из решения уравнений получим, что в таком случае b = 4: 5, а с = 3:5, пли что а: b: с — 5:4:3. Следовательно, условию задачи удовлетворяет любой египетский треугольник.

Правильное решение этой задачи прислала подписчики Э. Эллер, Б. Скрябин и М. Г. Грикуров.

Надо решить три помещенных здесь задачи №№ 43, 44, 45. Качество решений оценивается очками, согласно указаний в заголовках самих задач. Еще пол-очка дополнительно может быть прибавлено за тщательность и аккуратность в выполнении решений, при соблюдении, конечно, всех требуемых условий. Те участники конкурса, которые соберут в сумме наибольшее число очков, премируются следующими 10 премиями (при равенстве очков применяется жребий).