Юрченко Борисович - Философия и логика времени

IX. Психо-математика и фоновая зависимость

Необратимость времени логически эквивалентна причинности физического мира. Причинность физического мира в свою очередь логически требует мгновенного покоя, в котором ничто не происходит между причиной и следствием, поскольку без нее детерминизм невозможен. Нулевая точка мгновенного покоя эквивалента конечной скорости света. Конечная же скорость света (а вместе с ней и причинность, и точка покоя, и стрела времени) эквивалентна единственности нашей души. Из фантастических историй нам хорошо известно, что такое путешествие в прошлое (обычно герой использует для этого сверхсветовую скорость или кротовую нору в пространстве-времени) должно раздвоить его душу, ибо там он должен встретить самого себя, а изменив что-то в своей судьбе, получить того, кем он был, и того, кем он стал в новом ПС. А это уже, как минимум, две души и две Вселенной, не говоря уже про те души, которые персонаж тоже раздвоил, изменив их судьбы. Т.о. нарушение физических законов требует нарушения и ментальных законов, обеспечивающих единственность и уникальность наших душ в единственной и уникальной реальности. Назовем эти пять понятий «Звездой онтологии».

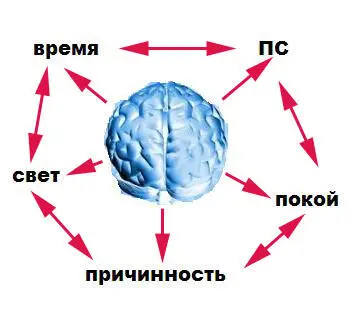
Рис.17

Они логически эквивалентны друг другу. Когда говорим: Время, - говорим: Причинность. Когда говорим: Причинность, - говорим: Покой. Когда говорим: Покой, - говорим: Свет. Когда говорим: Свет, - говорим: Душа. Когда говорим: Душа, - говорим: Время. Душа, напомним, – это по определению конечный отрезок ПС, который продолжает непрерывно прирастать новыми дхармами и может прекратиться только в смерти. Так какова должна быть участь этой души при свободном падении в черную дыру? Она ничего не заметит? В черной дыре душу ждет нирвана. Может ли она пройти через червоточину, раздвоиться в складках пространства-времени и увидеть свой клон в другом возрасте, т.е. в меньшем или большем наборе памяти, поскольку возраст индивида это – длина его ПС? Наш ответ: это абсолютно невозможно.

Математическое уравнение вида А + В = С , что бы ни подразумевалось за его компонентами и какими бы специализированными они ни были, всегда выглядит так, что в нем можно производить любые формально оправданные перестановки. А когда мы приравниваем его к нулю, А + В – С = 0 , то к чему в психологическом смысле мы его привязываем? Что есть этот нуль для мозга? Поскольку любое уравнение может представить в таком виде, то можно считать, что наше познание реальности и сама реальность возникают из ничего. Математическая и физическая реальность одинаковы абстрактны в мозге. Приравнивая уравнение к нулю, мы физически привязываем процесс к вечному настоящему (эфиру), а математически мы аннигилируем сущности в континууме, из которого извлекли их по собственной воле. Это диалектическое качество самосознания, которое проявляется в тождестве физической и психологической стрел времени и делает нашу логику адекватной причинности, наглядно отражено в алгебре, в теории групп и колец, где всегда присутствует множество обратных элементов и фундаментальный нуль (фундаментальная единица), к которому привязаны все элементы и которые «аннигилируют» в нем будто пара виртуальных частиц. Так что такое нуль?

Как и всякий объект самосознания, он есть по нашему определению дхарма. Какими атрибутами обладают дхармы помимо того, что в физическом времени они могут быть интерпретированы как мгновенный покой, который составляет для ПС его психологическое настоящее? Во-первых, все дхармы, как это утверждает гештальт-психология, целые. Этот атрибут очевиден. Если роза –это целый образ, то букет роз или лепесток розы – это тоже целые образы. Для самосознания не бывает полуцелых образов. Дхарма либо есть, либо ее нет. Но ПС может остановиться только в смерти, и поэтому какую-то дхарму мозг генерирует всегда, которая является целой в том смысле, в каком целым является любой бит информации. Это выражается и в том, что время для нас не обладает гамлетовским свойством быть или не быть. Оно не исчезает и не прекращается. Дхарма есть всегда.

Еще одним атрибутом дхармы является то, что она формируется как класс, как предикат. Роза – это не какая-то конкретная роза, это класс всех роз в мире, представленных некоторой дхармой, которую мы идентифицируем как розу вообще. В противном случае общение, язык и мышление были бы невозможны. Бессловесным существам оставалось бы только показывать друг другу физические предметы и мычать. В этом смысле мозг работает как исчисление предикатов, которое не интересуют отдельные объекты. Именно это выражено в платоновском идеализме, где идея (дхарма-класс) всегда преобладает над физическим индивидуальным объектом. Роза увянет, дхарма – никогда. Когда физик, например, говорит об электроне, он говорит об электроне вообще, т.е. о классе всех объектов, обладающих определенным свойством, а не о каком-то отдельном представителе этого семейства. Если история, в которой Уилер, размышляя о барионной асимметрии, заявил своему ученику Фейнману, что он нашел ей объяснение: «Во Вселенной есть лишь один-единственный электрон», - рассказывается скорее как анекдот, то мы вправе совершенно серьезно утверждать, что самосознание и даже все самосознания имеют дело с одним-единственным электроном-дхармой.

Самосознание всегда имеет независимый фон, подложку того, что оно дхармирует, независимо от того, сознает это человек или нет. Но именно поэтому всегда можно перейти на следующий уровень, сделав объектом рассмотрения фон, у которого автоматически появится новый фон. Математика изначально постулирует свой мир на нижнем уровне языка (дхарм): элементы и точки вводятся как неделимые по определению. При этом мысль уже не может двигаться вниз, но может двигаться вверх. Лишь затем из этих первичных сущностей создаются множества, пространства, функции и алгебры. Математика теоретически допускает множества множеств, множества множеств множеств и т.д. За бесконечностью возможны супербесконечности (трансфиниты). Пространства могут вкладываться в пространства и быть бесконечномерными. Структуру можно делать все сложнее и сложнее, но практически математика работает в очень небольшом языковом диапазоне. Кажется бессмысленным искусственно нагромождать сложности. Формально это, например, выражается в том, что в математике очень часто встречаются сущности вида Х n, т.е. некие величины с экспонентой, но очень редко встречаются величины, экспоненты которых имеют собственные экспоненты и совсем не встречаются такие, где экспонент еще больше.