Стивен Строгац - Удовольствие от Х

Однако всем поклонникам рациональности Евклида не хватает понимания интуитивных аспектов геометрии. Без вдохновения не было бы никаких доказательств или теорем, которые следует доказать в первую очередь. Как и при сочинении музыки или стихов, в геометрии требуется получить что-то из ничего. Как поэту найти нужные слова или композитору — западающую в память мелодию? Это тайна музыки; своя тайна присуща и математике.

В качестве иллюстрации рассмотрим задачу построения равностороннего треугольника. Правила игры заключаются в том, что вам дают одну сторону треугольника (отрезок), как показано на рисунке:

Ваша задача — найти способ использовать этот отрезок для построения двух других сторон и доказать, что у них такая же длина, как и у первой. Причем в вашем распоряжении только поверочная линейка и циркуль. Линейка позволяет начертить прямую линию любой длины или соединить прямой линией две любые точки. Циркуль помогает нарисовать окружность любого радиуса с центром в любой точке.

Однако имейте в виду, что это не обычная линейка: на ней нет делений и ее нельзя использовать для измерения длины. (Другими словами, она не подходит для копирования или измерения исходного отрезка.) Циркулем нельзя измерять углы, а можно только строить окружности.

Готовы? Поехали!

Вы в ступоре. С чего начать?

Логика здесь не поможет. Те, кому приходится часто принимать решения, знают, что в такой ситуации лучше всего расслабиться и попробовать разгадать головоломку в надежде, что что-нибудь придет в голову. Например, с помощью поверочной линейки попробовать через концы отрезка провести наклонные линии.

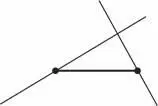
Не повезло. Хотя линии образуют треугольник, нет никакой гарантии, что он равносторонний .

Пытаемся провести несколько окружностей с помощью циркуля и опять попадаем пальцем в небо. Где выбрать центр окружности? В конечных точках отрезка?

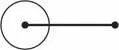
Или в какой-то его внутренней точке?

Второй вариант выглядит совершенно бесперспективным, поэтому нет смысла перебирать все внутренние точки отрезка одну за другой. Так что давайте вернемся к построению окружности вокруг конечных точек.

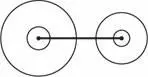
К сожалению, здесь много неопределенности. Какими должны быть радиусы окружностей? Что ж, пока мы ничего не смогли придумать.

Спустя несколько минут бесполезных размышлений вы, окончательно расстроившись, готовы сдаться. Но если мы все-таки устоим перед соблазном и продолжим, то нам, возможно, повезет, и мы поймем, что нужно построить всего одну окружность. Давайте посмотрим, что произойдет, если поставить иголку циркуля на один конец отрезка, карандаш на другой, а потом сделать циркулем полный оборот. Выйдет следующее:

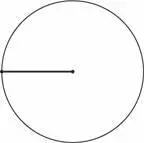
Конечно, если бы мы использовали в качестве центра окружности другую конечную точку, то получили бы другое изображение:

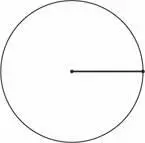
Как насчет того, чтобы одновременно нарисовать обе окружности без причины, просто ради интереса?

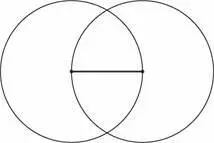
Вас словно током ударило? Вы даже задрожали от предвкушения? Взгляните еще раз на рисунок. Оттуда на нас «уставилось» соблазнительно округлое изображение равностороннего треугольника. Его верхний угол — точка пересечения окружностей.

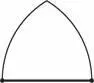
А теперь давайте превратим его в обычный прямосторонний треугольник, проведя линии через точку пересечения и конечные точки исходного треугольника. В результате треугольник выглядит точно так же, как равносторонний.

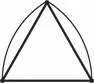
Мы позволили интуиции завести нас так далеко, что теперь и только теперь наступило время логике взяться за доказательство и завершить его. Для наглядности сделаем панорамную съемку полного изображения и промаркируем интересующие нас точки как A , B и C .

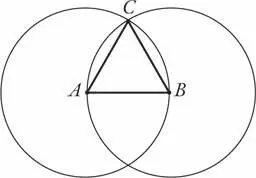
А вот и само доказательство. У сторон АС и ВС такая же длина, как и у исходного отрезка АВ , поскольку радиусы обеих окружностей равны длине отрезка AB . АС и ВС — радиусы окружностей, имеющие такую же длину. Следовательно, все три длины равны и треугольник является равносторонним. Что и требовалось доказать.

Идея с радиусами окружностей существует уже много столетий. Действительно, она открывает первую книгу евклидовых «Начал». Но укоренившаяся тенденция предлагать ученикам уже готовую окончательную схему с хитрыми окружностями лишает их радости открытия. Это педагогическая ошибка. Такой подход настраивает молодого человека на то, что идея очевидна. А ведь она может стать озарением для каждого нового поколения, если учить его правильно.

Конечно, ключом к данному доказательству было вдохновенное построение двух окружностей. С его помощью можно доказать еще одну, более известную теорему, которая звучит следующим образом: сумма углов треугольника равна 180°.

В этом случае лучшим будет не доказательство Евклида, а более раннее, приписываемое пифагорейцам. Делается это так. Рассмотрим любой треугольник и обозначим его углы, как a , b и c .

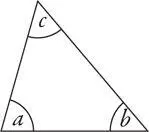
Через верхний угол треугольника проведем линию, параллельную основанию.

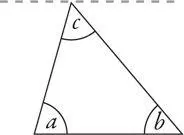
Теперь на секунду отвлечемся и вспомним свойства параллельных прямых: если третья прямая пересекает две параллельные прямые, как здесь,

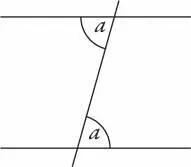
то углы, помеченные как а , равны.

Попробуем применить это свойство углов к сделанным выше построениям, в которых через вершину угла треугольника проведена прямая, параллельная его основанию.