Ричард Фейнман - 2. Пространство. Время. Движение

Фиг. 16.2. Упругое столкновение одинаковых тел, движущихся с равными скоростями в противоположных направлениях, при раз­личном выборе систем координат.

Далее, напомним, что одно и то же столкновение выглядит по-разному, смотря по тому, как повернуты оси. Для удобства мы так повернем оси, чтобы горизонталь делила пополам угол между направлениями частиц до и после столкновения (фиг. 16.2,б). Это то же столкновение, что и на фиг. 16.2,а, но с повернутыми осями.

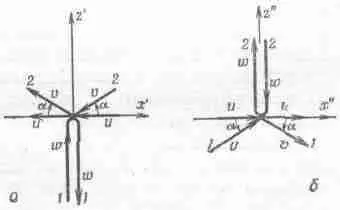
Теперь начинается самое главное: взглянем на это столкно­вение с позиций наблюдателя, движущегося на автомашине со скоростью, совпадающей с горизонтальной компонентой ско­рости одной из частиц. Как оно будет выглядеть? Наблюдателю покажется, что частица 1 поднимается прямо вверх (горизон­тальная компонента у нее пропала), а после столкновения падает прямо вниз по той же причине (фиг. 16.3, а).

Фиг. 16.3. Еще две картины того же столкновения (видимые из дви­жущихся автомашин).

Зато частица 2 движется совсем иначе, она проносится мимо с колоссальной скоростью и под малым углом (но этот угол и до и после столк­новения одинаков). Обозначим горизонтальную компоненту скорости частицы 2 через и, а вертикальную скорость части­цы 1 — через w.

Чему же равна вертикальная скорость utga частицы 2? Зная это, можно получить правильное выражение для импульса, пользуясь сохранением импульса в вертикальном направлении. (Сохранение горизонтальной компоненты импульса и так обеспечено: у обеих частиц до и после столкновения эта ком­понента одинакова, а у частицы 1 она вообще равна нулю. Так что следует требовать только сохранения вертикальной скорости utga.) Но вертикальную скорость можно получить, просто взглянув на это столкновение с другой точки зрения! Посмотрите на столкновение, изображенное на фиг. 16.3, а из автомашины, которая движется теперь налево со скоростью и. Вы увидите то же столкновение, но перевернутое «вверх ногами» (фиг. 16.3, б). Теперь уже частица 2 упадет и подскочит со скоростью w, а горизонтальную скорость и приобретет частица 1. Вы уже, конечно, догадываетесь, чему равна горизонтальная скорость utg a ; она равна wЦ(1- u 2/c 2) [см. уравнение (16.7)]. Кроме того, нам известно, что изменение вертикального им­пульса вертикально движущейся частицы равно

D p=2m w w

(двойка здесь потому, что движение вверх перешло в движение вниз). У частицы, движущейся косо, скорость равна v, ее компоненты равны uи wЦ(1-u 2 /c 2 ), а масса ее m v . Изменение вертикального импульса этой частицы D р'=2т v wЦ( 1—u 2/с 2), так как в соответствии с нашим предположением (16.8) любая компонента импульса равна произведению одноименной ком­поненты скорости на массу, отвечающую этой скорости. Но суммарный импульс равен нулю. Значит, и вертикальные импульсы должны взаимно сократиться, отношение же массы, движущейся со скоростью w, к массе, движущейся со скоростью v, должно оказаться равным

m w/m v=Ц(1-u 2/c 2). (16.9).

Перейдем к предельному случаю, когда w стремится к нулю. При очень малых w величины v и u практически совпадут, m w ®m 0 , a m v ®m u . Окончательный результат таков:

Проделайте теперь такое интересное упражнение: проверьте, будет ли выполнено условие (16.9) при произвольных w , когда масса подчиняется формуле (16.10). При этом скорость v, стоящую в уравнении (16.9), можно найти из прямоугольного треугольника

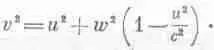
Вы увидите, что (16.9) выполняется тождественно, хотя выше нам понадобился только предел этого равенства при w—>0. Теперь перейдем к дальнейшим следствиям, считая уже, что, согласно (16.10), масса зависит от скорости. Рассмотрим так называемое неупругое столкновение. Для простоты пред­положим, что из двух одинаковых тел, сталкивающихся с равными скоростями w, образуется новое тело, которое больше не распадается (фиг. 16.4,а).

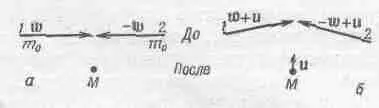
Фиг. 16.4. Две картины неупругого соударения тел равной массы.

Массы тел до столкновения равны, как мы знаем, m 0 /Ц(1- w 2 /c 2 ). Предположив сохраня­емость импульса и приняв принцип относительности, можно продемонстрировать интересное свойство массы вновь образо­ванного тела. Представим себе бесконечно малую скорость и, поперечную к скоростям w (можно было бы работать и с ко­нечной скоростью и, но с бесконечно малым значением и легче во всем разобраться), и посмотрим на это столкновение, дви­гаясь в лифте со скоростью - u. Перед нами окажется картина, изображенная на фиг. 16.4, а. Составное тело обладает неиз­вестной массой М. У тела 1, как и у тела 2, есть компонента скорости и, направленная вверх, и горизонтальная компонента, практически равная w. После столкновения остается масса М, движущаяся вверх со скоростью u, много меньшей и скорости света и скорости w. Импульс должен остаться прежним; по­смотрим поэтому, каким он был до столкновения и каким стал потом. До столкновения он был равен p~=2m w u, а потом стал р'=M u u. Но M u из-за малости u , по существу, совпадает с М 0. Благодаря сохранению импульса

М 0=2m w. (16.11)

Итак, масса тела, образуемого при столкновении двух одина­ковых тел, равна их удвоенной массе. Вы, правда, можете сказать: «Ну и что ж, это просто сохранение массы». Но не торопитесь восклицать: «Ну и что ж!», потому что сами-то массы тел были больше, чем когда тела неподвижны. Они вносят в суммарную массу М не массу покоя, а больше. Не правда ли, поразительно! Оказывается, сохранение импульса в столк­новении двух тел требует, чтобы образуемая ими масса была больше их масс покоя, хотя после столкновения эти тела сами придут в состояние покоя!

§ 5. Релятивистская энергия

Немного выше мы показали, что зависимость массы от скорости и законы Ньютона приводят к тому, что изменения в кинетической энергии тела, появляющиеся в результате работы приложенных к нему сил, оказываются всегда равными