Ричард Фейнман - 2. Пространство. Время. Движение

Это так называемая теорема о центре масс, и доказывается она следующим образом.

Любой объект можно рассматривать как множество малень­ких частичек, атомов, связанных различными силами. Пусть i обозначает номер одной из таких частиц (их страшно много, по­этому i может быть равно, например, 10 23). Сила, действующая на i-ю частицу, равна массе, умноженной на ускорение этой частицы:

В последующих главах наши движущиеся объекты и все их части будут двигаться со скоростями, много меньшими, чем скорость света, и поэтому для всех величин мы будем рас­сматривать только нерелятивистское приближение. Масса при этих условиях будет постоянна, так что

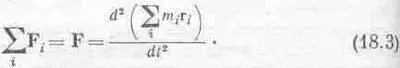
Если теперь сложить все силы, действующие на частицы, т. е. сложить все F i- со всеми значениями индекса, то в результате мы должны получить полную силу F. Складывая же правые части уравнения (18.2) для всех частиц и вспоминая, что про­изводная от суммы равна сумме производных, получаем

Поэтому полная сила равна второй производной от суммы произведений масс частиц на их положение.

Но полная сила, действующая на все частицы,— это то же самое, что и внешняя сила. Почему? Да потому что, какие бы силы ни действовали между частицами, пусть это будет притя­жение или отталкивание, или атомные силы, все равно, когда мы складываем их вместе и применяем Третий закон Ньютона, по которому силы действия и противодействия между любыми двумя частицами равны друг другу, то эти взаимные силы сокращаются друг с другом и в результате останутся только силы, действующие со стороны атомов, находящихся вне тела. Так что, если уравнение (18.3) представляет собой сумму по некоторому числу частиц, образующих наш объект, то внешняя сила, действующая на него, равна просто сумме всех сил, действующих на все частицы, образующие этот объект. Урав­нение (18.3) неплохо было бы записать в виде полной массы тела, умноженной на какое-то ускорение. Сделать это можно. Пусть М будет суммой масс всех частиц, т. е. полной массой тела. Если теперь определить вектор Rкак

то, поскольку М постоянна, уравнение (18.3) перейдет в

Таким образом, внешняя сила равна полной массе, умно­женной на ускорение некоторой точки R; эта точка и называ­ется центром масс тела. Она расположена где-то в «середине» тела — некое среднее r, в котором различные r iучитываются в зависимости от их важности, т. е. в зависимости от того, какую долю вносят они в полную массу.

Мы подробно обсудим эту важную теорему несколько позд­нее, а сейчас остановимся на двух примерах. Пусть на тело не действуют никакие внешние силы, скажем, оно плавает где-то в пустом пространстве. Оно может делать все, что ему угодно: крутиться, покачиваться, изгибаться, но при этом его центр масс, эта искусственно выделенная нами математическая точка, должен двигаться, с постоянной скоростью. В частности, если вначале этот центр покоился, то он так и будет покоиться все время. Поэтому если мы возьмем какой-то космический корабль со всеми его пассажирами, вычислим его центр масс и обна­ружим, что он стоит на месте, то можно быть уверенным, что центр масс так и останется на месте, если только на корабль не будут воздействовать какие-то внешние силы. Сам корабль, конечно, может немного перемещаться, но это потому, что пассажиры внутри корабля ходят взад и вперед. Так, если все пассажиры одновременно перейдут в носовую часть, то корабль немного подастся назад, чтобы среднее положение всех масс осталось в точности на том же самом месте.

Означает ли это, что в результате неподвижности центра масс ракета не может двигаться вперед? Конечно, нет, но, чтобы продвинуть вперед интересующую нас часть ракеты, мы что-то должны выбросить назад. Иными словами, если вна­чале ракета покоилась, а затем выбросила из сопла некоторое количество газа, то газ этот полетит назад, а сама ракета по­летит при этом вперед, однако центр масс останется точно на том же месте, где он был и раньше. Так что в ракете интере­сующая нас часть продвинется вперед за счет другой, которая улетит назад.

Второе замечание относительно движения центра масс. Его можно рассматривать отдельно от всех «внутренних» дви­жений тела и, следовательно, его можно не учитывать при изучении вращения. Собственно поэтому мы начали изучать вращения с центра масс.

§ 2. Вращение твердого тела

Поговорим теперь о вращении. Как известно, обычные предметы не вращаются просто так: они колеблются, вибри­руют, изгибаются. Поэтому, чтобы упростить рассуждения, рассмотрим движение несуществующего идеального объекта, который мы назвали твердым телом. В таком объекте связи между атомами столь сильны, что те небольшие силы, которые необходимы, чтоб привести его в движение, не могут деформи­ровать тело. Форма его все время остается одной и той же. Если мы хотим изучить движение такого тела и условимся не принимать во внимание движение его центра масс, то ему остается лишь вращаться. Вот это вращение мы и должны описать. Каким образом? Предположим, что в теле существует какая-то воображаемая неподвижная линия (она может про­ходить через центр масс, а может и не проходить); вокруг этой линии, как вокруг оси, вращается наше тело. Но как все-таки определить, что такое вращение? Сделать это совсем просто. Отметив какую-то точку на теле, где угодно, только не на оси, и зная, куда она перешла через некоторый промежуток времени, мы точно можем сказать, в каком положении находится тело. Единственное, что нужно знать для описания положения точки, - это угол. Таким образом, изучение вращения заключается в изучении изменения угла со временем.

Чтобы описать вращение, измерим угол, на который пово­рачивается тело. Разумеется, речь идет не об угле между двумя точками внутри самого тела или на теле, а об угловом изме­нении положения всего тела как целого от одного момента вре­мени до другого.

Сначала давайте разберемся с кинематикой вращения. Изменение угла со временем очень похоже на изменение по­ложения при одномерном движении; для плоского вращения мы можем говорить об угловом положении и угловой скорости. Между этими двумя движениями — плоским вращением и одномерным перемещением — существует очень интересная связь: почти каждая величина в одном случае имеет свой аналог в другом. Прежде всего угол q, указывающий, насколько повернулось тело, соответствует пройденному точкой расстоя­нию s. Угловая скорость w =d q /dt, которая показывает, с какой быстротой изменяется угол, соответствует обычной скорости v=ds/dt, описывающей быстроту изменения положения. Если угол измеряется в радианах, то угловая скорость w равна какому-то числу радиан в секунду. Чем больше угловая ско­рость, тем быстрее вращается объект и тем быстрее изменяется угол. Если продифференцировать угловую скорость по вре­мени, то получим величину a=d w /dt, которую мы будем на­зывать угловым ускорением. Оно может служить аналогом обычного ускорения.