Нихиль Будума - Основы глубокого обучения

Почему некоторые задачи компьютерам решать тяжело? Стандартные программы доказали свою состоятельность в двух областях: 1) они очень быстро ведут вычисления; 2) они неукоснительно следуют инструкциям. Если вы финансист и вам нужно провести сложные математические подсчеты, вам повезло. Типовые программы вам в помощь. Но представьте себе, что нам нужно сделать кое-что поинтереснее: например, написать программу для автоматического распознавания почерка. Возьмем за основу рис. 1.1.

Рис. 1.1. Изображение из массива рукописных данных MNIST [2] LeCun Y., Bottou L., Bengio Y., Haffner P. Gradient-Based Learning Applied to Document Recognition // Proceedings of the IEEE. 1998. November. Vol. 86 (11). Pp. 2278–2324.

Хотя каждая цифра на рисунке слегка отличается от предыдущей, мы легко опознаем в первом ряде нули, во втором — единицы и т. д. Теперь напишем компьютерную программу, которая решит ту же задачу. Какие правила нужно задать, чтобы различать цифры?

Начнем с простого. Например, укажем, что нулю соответствует изображение округлого замкнутого контура. Все примеры с рис. 1.1 Рис. 1.1. Изображение из массива рукописных данных MNIST [2] LeCun Y., Bottou L., Bengio Y., Haffner P. Gradient-Based Learning Applied to Document Recognition // Proceedings of the IEEE. 1998. November. Vol. 86 (11). Pp. 2278–2324. Хотя каждая цифра на рисунке слегка отличается от предыдущей, мы легко опознаем в первом ряде нули, во втором — единицы и т. д. Теперь напишем компьютерную программу, которая решит ту же задачу. Какие правила нужно задать, чтобы различать цифры? Начнем с простого. Например, укажем, что нулю соответствует изображение округлого замкнутого контура. Все примеры с рис. 1.1 , кажется, удовлетворяют этому определению, но таких признаков недостаточно. Что, если у кого-то ноль — не всегда замкнутая фигура? И как отличить такой ноль (см. рис. 1.2) от шестерки? Рис. 1.2. Ноль, алгоритмически трудноотличимый от шестерки Можно задать рамки расстояния между началом и концом петли, но не очень понятно какие. И это только начало проблем. Как различить тройки и пятерки? Четверки и девятки? Можно добавлять правила, или признаки , после тщательных наблюдений и месяцев проб и ошибок, но понятно одно: процесс будет нелегок. Многие другие классы задач попадают в ту же категорию: распознавание объектов и речи, автоматический перевод и т. д. Мы не знаем, какие программы писать для них, потому что не понимаем, как с этим справляется наш мозг. А если бы и знали, такая программа была бы невероятно сложной. , кажется, удовлетворяют этому определению, но таких признаков недостаточно. Что, если у кого-то ноль — не всегда замкнутая фигура? И как отличить такой ноль (см. рис. 1.2) от шестерки?

Рис. 1.2. Ноль, алгоритмически трудноотличимый от шестерки

Можно задать рамки расстояния между началом и концом петли, но не очень понятно какие. И это только начало проблем. Как различить тройки и пятерки? Четверки и девятки? Можно добавлять правила, или признаки , после тщательных наблюдений и месяцев проб и ошибок, но понятно одно: процесс будет нелегок.

Многие другие классы задач попадают в ту же категорию: распознавание объектов и речи, автоматический перевод и т. д. Мы не знаем, какие программы писать для них, потому что не понимаем, как с этим справляется наш мозг. А если бы и знали, такая программа была бы невероятно сложной.

Для решения таких задач нужен совсем иной подход. Многое из того, что мы усваиваем в школе, похоже на стандартные компьютерные программы. Мы учимся перемножать числа, решать уравнения и получать результаты, следуя инструкциям. Но навыки, которые мы получаем в самом юном возрасте и считаем самыми естественными, усваиваются не из формул, а на примерах.

Например, в двухлетнем возрасте родители не учат нас узнавать собаку, измеряя форму ее носа или контуры тела. Мы можем отличать ее от других существ, потому что нам показали много примеров собак и несколько раз исправили наши ошибки. Уже при рождении мозг дал нам модель, описывающую наше мировосприятие. С возрастом благодаря ей мы стали на основе получаемой сенсорной информации строить предположения о том, с чем сталкиваемся. Если предположение подтверждалось родителями, это способствовало укреплению модели. Если же они говорили, что мы ошиблись, мы меняли модель, дополняя ее новой информацией. С опытом она становится все точнее, поскольку включает больше примеров. И так происходит на подсознательном уровне, мы этого даже не понимаем, но можем с выгодой использовать.

Глубокое обучение — отрасль более широкой области исследований искусственного интеллекта: машинного обучения , подразумевающего получение знаний из примеров. Мы не задаем компьютеру огромный список правил решения задачи, а предоставляем модель , с помощью которой он может сравнивать примеры, и краткий набор инструкций для ее модификации в случае ошибки. Со временем она должна улучшиться настолько, чтобы решать поставленные задачи очень точно.

Перейдем к более строгому изложению и сформулируем идею математически. Пусть наша модель — функция h ( x, θ). Входное значение x— пример в векторной форме. Допустим, если x— изображение в оттенках серого, компоненты вектора — интенсивность пикселей в каждой позиции, как показано на рис. 1.3.

Рис. 1.3. Векторизация изображения для алгоритма машинного обучения

Входное значение θ — вектор параметров, используемых в нашей модели. Программа пытается усовершенствовать их значения на основе растущего числа примеров. Подробнее мы рассмотрим этот вопрос в главе 2.

Чтобы интуитивно понимать модели машинного обучения, рассмотрим пример. Допустим, мы решили узнать, как предсказывать результаты экзаменов, если известно количество часов сна и учебы в день перед испытанием. Мы собираем массив данных и при каждом замере х = [ x 1x 2 ] T записываем количество часов сна ( x 1), учебы ( x 2) и отмечаем, выше или ниже они средних по классу. Наша цель — создать модель h(х ,θ ) с вектором параметров θ = [θ 0θ 1θ 2] T , чтобы:

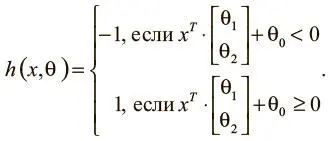
По нашему предположению, проект модели h(х ,θ ) будет таким, как описано выше (с геометрической точки зрения он описывает линейный классификатор, делящий плоскость координат надвое). Теперь мы хотим узнать вектор параметров θ, чтобы научить модель делать верные предсказания (−1, если результаты ниже среднего уровня, и 1 — если выше) на основании примерного входного значения x. Такая модель называется линейным персептроном и используется с 1950-х [3] Rosenblatt F. The perceptron: A probabilistic model for information storage and organization in the brain // Psychological Review. 1958. Vol. 65. No. 6. P. 386. . Предположим, наши данные соответствуют тому, что показано на рис. 1.4.