Нихиль Будума - Основы глубокого обучения

На практике для вычислений применяются три типа нелинейных нейронов. Первый называется сигмоидным и использует функцию:

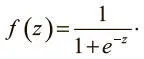
Интуитивно это означает, что, если логит очень мал, выходные данные логистического нейрона близки к 0. Если логит очень велик — то к 1. Между этими двумя экстремумами нейрон принимает форму буквы S, как на рис. 1.11.

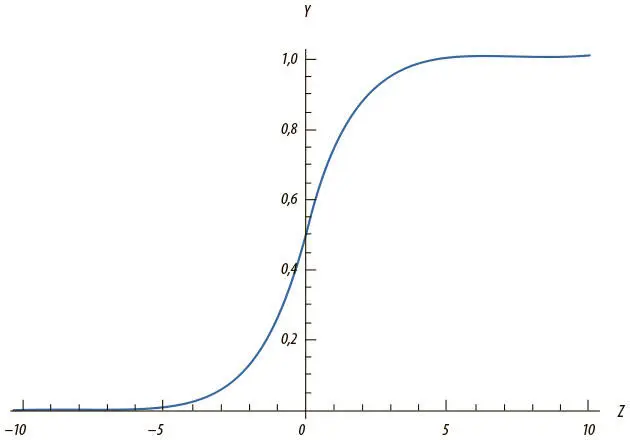
Рис. 1.11. Выходные данные сигмоидного нейрона с переменной z

Нейроны гиперболического тангенса (tanh-нейроны) используют похожую S-образную нелинейность, но исходящие значения варьируют не от 0 до 1, а от −1 до 1. Формула для них предсказуемая: f(z) = tanh( z ). Отношения между входным значением y и логитом z показаны на рис. 1.12. Когда используются S-образные нелинейности, часто предпочитают tanh-нейроны, а не сигмоидные, поскольку у tanh-нейронов центр находится в 0.

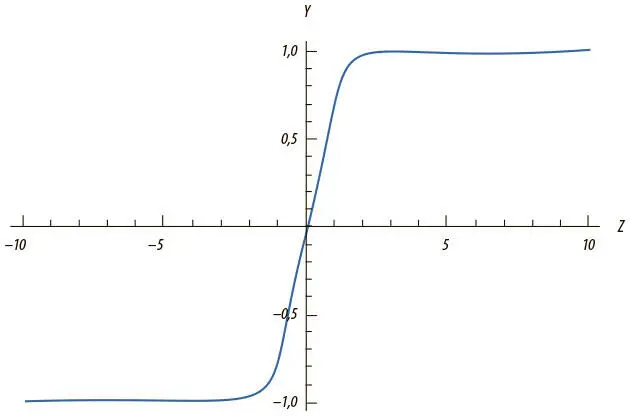
Рис. 1.12. Выходные данные tanh-нейрона с переменной z

Еще один тип нелинейности используется нейроном с усеченным линейным преобразованием (ReLU) . Здесь задействована функция f(z) = max(0, z ), и ее график имеет форму хоккейной клюшки (рис. 1.13).

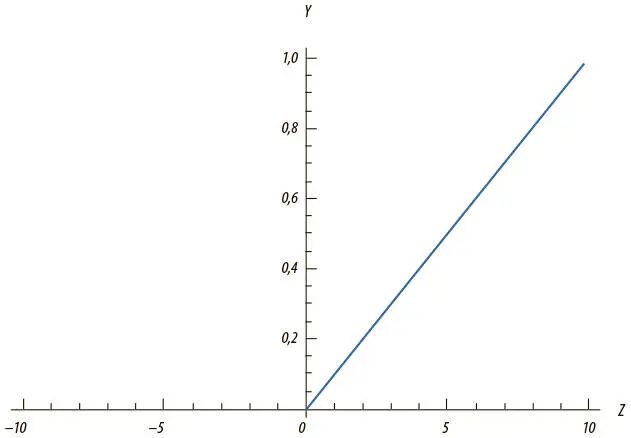
Рис. 1.13. Выходные данные ReLU-нейрона с переменной z

ReLU в последнее время часто выбирается для выполнения многих задач (особенно в системах компьютерного зрения) по ряду причин, несмотря на свои недостатки [8]. Этот вопрос мы рассмотрим в главе 5 вместе со стратегиями борьбы с потенциальными проблемами.

Часто нужно, чтобы выходной вектор был распределением вероятностей по набору взаимоисключающих значений. Допустим, нам нужно создать нейросеть для распознавания рукописных цифр из набора данных MNIST. Каждое значение (от 0 до 9) исключает остальные, но маловероятно, чтобы нам удалось распознать цифры со стопроцентной точностью. Распределение вероятностей поможет понять, насколько мы уверены в своих выводах. Желаемый выходной вектор приобретает такую форму, где :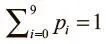

[p 0 p 1 p 2 p 3… p 9 ] .

Для этого используется особый выходной слой, именуемый слоем с мягким максимумом (softmax) . В отличие от других типов, выходные данные нейрона в слое с мягким максимумом зависят от выходных данных всех остальных нейронов в нем. Нам нужно, чтобы сумма всех выходных значений равнялась 1. Приняв z i как логит i -го нейрона с мягким максимумом, мы можем достичь следующей нормализации, задав выходные значения:

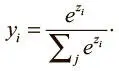
При сильном предсказании одно из значений вектора будет близко к 1, остальные — к 0. При слабом останется несколько возможных значений, каждое из которых характеризуется своим уровнем вероятности.

В этой главе мы дали базовые представления о машинном обучении и нейросетях. Мы рассказали о структуре нейрона, работе нейросетей с прямым распространением сигнала и важности нелинейности в решении сложных задач обучения. В следующей главе мы начнем создавать математический фундамент для обучения нейросети решению задач. Например, мы поговорим о нахождении оптимальных векторов параметров, лучших методов обучения нейросетей и основных проблемах. В последующих главах мы будем применять эти основополагающие идеи к более специализированным вариантам архитектуры нейросетей.

Мы начинаем понимать, как решать некоторые интересные задачи с помощью глубокого обучения, но остается важный вопрос: как определить, какими должны быть векторы параметров (веса всех соединений нейросети)? Ответ прост: в ходе процесса, часто именуемого обучением (рис. 2.1). Мы демонстрируем нейросети множество обучающих примеров и последовательно модифицируем веса, чтобы минимизировать ошибки, которые уже были совершены. Продемонстрировав достаточное число примеров, мы ожидаем, что нейросеть будет эффективно решать поставленную задачу.

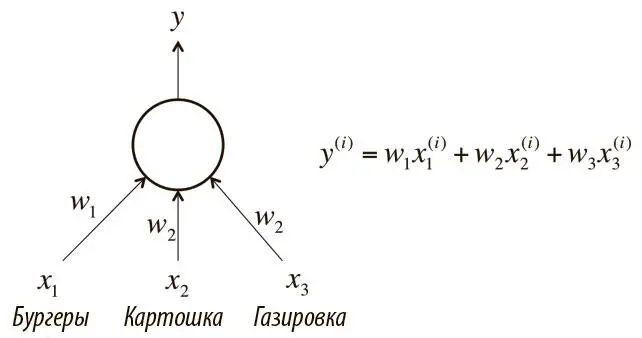
Рис. 2.1. Нейрон, который мы хотим обучить решать проблему фастфуда

Вернемся к примеру, который упоминали в предыдущей главе при обсуждении линейного нейрона. Итак: каждый день мы покупаем в ресторане быстрого обслуживания обед — бургеры, картошку и газировку, причем по несколько порций каждого наименования. Мы хотим предсказывать, сколько будет стоить обед, но ценников нет. Кассир сообщает только общую цену.

Мы хотим обучить один линейный нейрон решать эту задачу. Как?

Один из вариантов — разумно подбирать примеры для обучения. Для одного обеда купим один бургер, для второго — одну порцию картошки, для третьего — один стакан газировки. В целом разумный подбор примеров — хорошая идея. Многие исследования показывают, что, создав хорошую подборку данных для обучения, вы сможете заметно повысить эффективность нейросети. Но проблема использования только этого подхода в том, что в реальных ситуациях он редко приближает нас к решению. Например, при распознавании изображений аналога ему нет и решения мы не найдем.

Нам нужно найти вариант, который поможет решать задачу в общем случае. Допустим, у нас очень большой набор обучающих примеров. Это позволит нам вычислить, какие выходные значения выдаст нейросеть на i -м примере, при помощи простой формулы. Мы хотим обучить нейрон и подбираем оптимальные веса, чтобы свести к минимуму ошибки при распознавании примеров. Можно сказать, мы хотим свести к минимуму квадратичную ошибку во всех примерах, которые встретим. Формально, если мы знаем, что t (i) — верный ответ на i -й пример, а y (i) — значение, вычисленное нейросетью, мы хотим свести к минимуму значение функции потерь E :

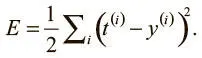
Квадратичная ошибка равна 0, когда модель дает корректные предсказания для каждого обучающего примера. Более того, чем ближе E к 0, тем лучше модель. Наша цель — выбрать такой вектор параметров θ (значения всех весов в этой модели), чтобы E было как можно ближе к 0.