Нихиль Будума - Основы глубокого обучения

Рис. 1.4. Образец данных для алгоритма предсказания экзаменов и потенциального классификатора

Оказывается, при θ = [−24 3 4] T модель машинного обучения способна сделать верное предсказание для каждого замера:

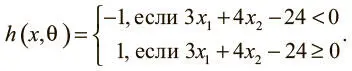
Оптимальный вектор параметров θ устанавливает классификатор так, чтобы можно было сделать как можно больше корректных предсказаний. Обычно есть множество (иногда даже бесконечное) возможных оптимальных вариантов θ. К счастью, в большинстве случаев альтернативы настолько близки, что разницей между ними можно пренебречь. Если это не так, можно собрать больше данных, чтобы сузить выбор θ.

Звучит разумно, но есть много очень серьезных вопросов. Во-первых, откуда берется оптимальное значение вектора параметров θ? Решение этой задачи требует применения метода оптимизации . Оптимизаторы стремятся повысить производительность модели машинного обучения, последовательно изменяя ее параметры, пока погрешность не станет минимальной.

Мы подробнее расскажем об обучении векторов параметров в главе 2, описывая процесс градиентного спуска [4] Bubeck S. Convex optimization: Algorithms and complexity // Foundations and Trends® in Machine Learning. 2015. Vol. 8. No. 3–4. Pp. 231–357. . Позже мы постараемся найти способы еще больше увеличить эффективность этого процесса.

Во-вторых, очевидно, что эта модель (линейного персептрона) имеет ограниченный потенциал обучения. Например, случаи распределения данных на рис. 1.5 нельзя удобно описать с помощью линейного персептрона.

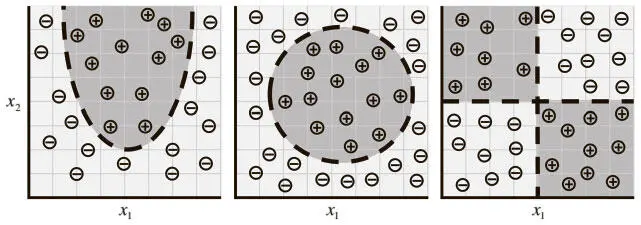
Рис. 1.5. По мере того как данные принимают более комплексные формы, нам становятся необходимы более сложные модели для их описания

Но эти ситуации — верхушка айсберга. Когда мы переходим к более комплексным проблемам — распознаванию объектов или анализу текста, — данные приобретают очень много измерений, а отношения, которые мы хотим описать, становятся крайне нелинейными. Чтобы отразить это, в последнее время специалисты по машинному обучению стали строить модели, напоминающие структуры нашего мозга. Именно в этой области, обычно называемой глубоким обучением, ученые добились впечатляющих успехов в решении проблем компьютерного зрения и обработки естественного языка. Их алгоритмы не только значительно превосходят все остальные, но даже соперничают по точности с достижениями человека, а то и превосходят их.

Нейрон — основная единица мозга. Небольшой его фрагмент, размером примерно с рисовое зернышко, содержит более 10 тысяч нейронов, каждый из которых в среднем формирует около 6000 связей с другими такими клетками [5] Restak R. M., Grubin D. The Secret Life of the Brain. Joseph Henry Press, 2001. . Именно эта громоздкая биологическая сеть позволяет нам воспринимать мир вокруг. В этом разделе наша задача — воспользоваться естественной структурой для создания моделей машинного обучения, которые решают задачи аналогично. По сути, нейрон оптимизирован для получения информации от «коллег», ее уникальной обработки и пересылки результатов в другие клетки. Процесс отражен на рис. 1.6. Нейрон получает входную информацию по дендритам — структурам, напоминающим антенны. Каждая из входящих связей динамически усиливается или ослабляется на основании частоты использования (так мы учимся новому!), и сила соединений определяет вклад входящего элемента информации в то, что нейрон выдаст на выходе. Входные данные оцениваются на основе этой силы и объединяются в клеточном теле . Результат трансформируется в новый сигнал, который распространяется по клеточному аксону к другим нейронам.

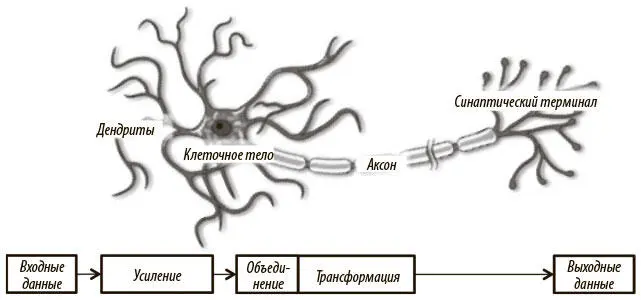
Рис. 1.6. Функциональное описание биологической структуры нейрона

Мы можем преобразовать функциональное понимание работы нейронов в нашем мозге в искусственную модель на компьютере. Последняя описана на рис. 1.7, где применен подход, впервые введенный в 1943 году Уорреном Маккаллоу и Уолтером Питтсом [6] McCulloch W. S., Pitts W. A logical calculus of the ideas immanent in nervous activity // The Bulletin of Mathematical Biophysics. 1943. Vol. 5. No. 4. Pp. 115–133. . Как и биологические нейроны, искусственный получает некоторый объем входных данных — x 1, x 2, …, x n , каждый элемент которых умножается на определенное значение веса — w 1, w 2, …, w n . Эти значения, как и раньше, суммируются, давая логит нейрона: 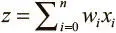. Часто он включает также смещение (константа, здесь не показана). Логит проходит через функцию активации f , образуя выходное значение y = f(z) . Это значение может быть передано в другие нейроны.

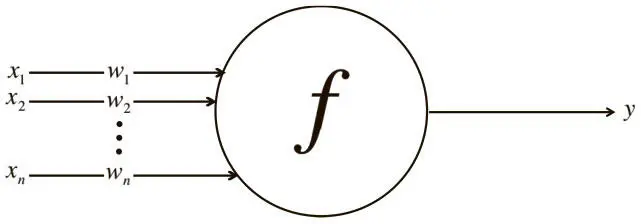
Рис. 1.7. Схема работы нейрона в искусственной нейросети

Математическое обсуждение искусственного нейрона мы закончим, выразив его функции в векторной форме. Представим входные данные нейрона как вектор x = [ x 1 x 2… x n ], а веса нейрона как w = [ w 1 w 2… w n ]. Теперь выходные данные нейрона можно выразить как y = f ( x w + b) , где b — смещение. Мы способны вычислить выходные данные из скалярного произведения входного вектора на вектор весов, добавив смещение и получив логит, а затем применив функцию активации. Это кажется тривиальным, но представление нейронов в виде ряда векторных операций очень важно: только в таком формате их используют в программировании.

Выше мы говорили об использовании моделей машинного обучения для определения зависимости между результатом на экзаменах и временем, потраченным на обучение и сон. Для решения задачи мы создали линейный классификатор-персептрон, который делит плоскость декартовых координат надвое:

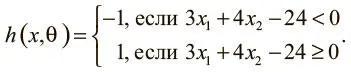
Как показано на рис. 1.4, это оптимальный вариант для θ: он позволяет корректно классифицировать все примеры в нашем наборе данных. Здесь мы видим, что наша модель h работает по образцу нейрона. Посмотрите на нейрон на рис. 1.8. У него два входных значения, смещение, и он использует функцию:

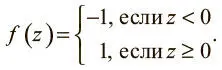
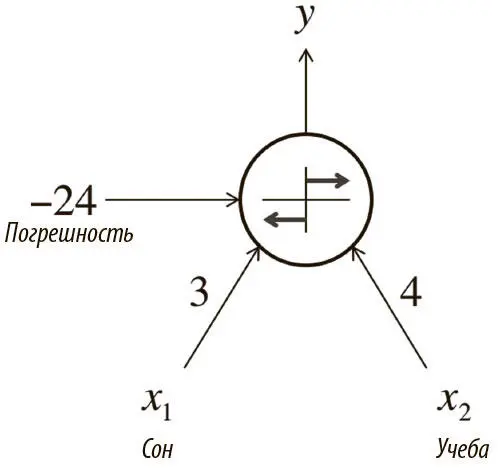
Рис. 1.8. Выражение результатов экзамена в виде нейрона